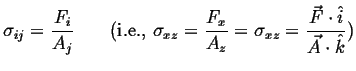 |
(07-1) |
A spring is an example of a one-dimensional material--it resists or exerts force in one direction only. A volume of material can exert forces in all three directions simultaneously--and the forces need not be the same in all directions. A volume of material can also be ``squeezed'' in many different ways: it can be squeezed in only one or in only two directions1
All the ways that a force can be applied to small element of material is illustrated below. A force divided by an area is a stress--think of it the area density of force.
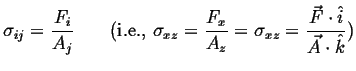 |
(07-1) |
![]() is a plane with normal in
is a plane with normal in
![]() -direction (or the projection of the area
of a plane
-direction (or the projection of the area
of a plane
![]() in the direction parallel to the
in the direction parallel to the
![]() )
)
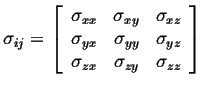 |
(07-2) |
There is one special and very simple case of elastic stress, and that is
called the hydrostatic stress.
It is the case of pure pressure and there are no shear (off-diagonal) stresses.
(i.e., all
![]() for
for
![]() , and
, and
![]() ).
An equilibrium system composed of a body in a fluid environment is always in hydrostatic stress:
).
An equilibrium system composed of a body in a fluid environment is always in hydrostatic stress:
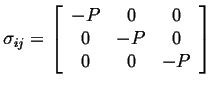 |
(07-3) |
If the body that is being stressed hydrostatically is isotropic, then its response is pure dilation (in other words, it expands or shrinks uniformly and without shear):
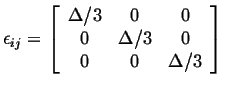 |
(07-4) |
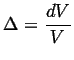 |
(07-5) |
So, for the case of hydrostatic stress, the work term has a particularly simple form:
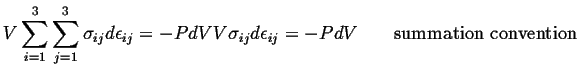 |
(07-6) |
This expression is the same as the rate of work performed on a compressible fluid, such as an ideal gas.