As part of our discussion of different ways that the internal
energy of a body
![]() could be changed, we considered what would
happen to a material if it is held in an electric field. In an
electric field, charges of opposite sign move in opposite directions, so
one side of the material takes on a different charge than another side--in other
words, it becomes polarized.
could be changed, we considered what would
happen to a material if it is held in an electric field. In an
electric field, charges of opposite sign move in opposite directions, so
one side of the material takes on a different charge than another side--in other
words, it becomes polarized.
Question: Do you think the internal energy of the material increases or decreases as it gets polarized? What about the energy associated with the device that creates the electric field?
Models for Anisotropic Polarizable Materials
We discussed a model for isotropic polarizable
materials--we wrote down an expression for the work of polarizing
a material in an electric field and then assumed linear isotropic
behavior to find an expression for the polarization energy in
such an idealized material.
We introduced a material parameter
![]() that quantifies how
much internal polarization develops for an applied electric field:
that quantifies how
much internal polarization develops for an applied electric field:
![]() .
.
In an isotropic material, therefore, the underlying material cannot influence the material response and the induced polarization, total polarization, and applied field are all parallel.
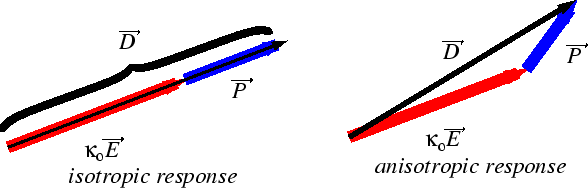 |
In an anisotropic material, the material response depends on the relative direction of the applied field and the crystal orientation--physically, the internal dipoles are constrained to lie in particular directions with respect to the underlying material.
The polarization is not necessarily in the direction of the field. The polarization is linearly related to the field direction.
Such linear relationships can be written as follows:
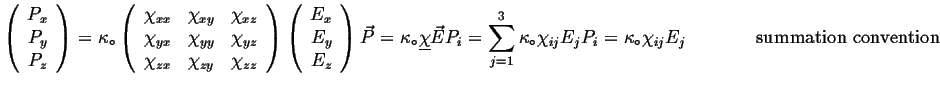 |
(07-7) |
where
![]() is called the the dielectric susceptibility tensor.
is called the the dielectric susceptibility tensor.
You won't be tested or otherwise asked whether you understand what a tensor is in this course, but I will tell you what they are because they are important. They are representations of materials properties that may depend on the underlying symmetry of the material--or any measurable quantity that can depend on the orientation of the measuring device with respect to some laboratory coordinate system.
| Tensors |
| Extraneous but Potentially Instructive Material |
|
A tensor expresses the relation between material response or force with
respect to the axes of its underlying symmetry to the axes of
response or force in a laboratory frame.
A first rank tensor is a spatial vector: its three components refer to the axes of some reference frame. A second rank tensor has 9 components, like a matrix. Each component is associated with two axes: one from the set of the reference frame axes and one from the material frame axes. You can think of the second rank tensor as a linear relationship between two vectors (or equivalently, two first rank tensors). A third rank tensor is a relationship between a first rank tensor and a second rank tensor, and so on.
An
|
When a material property is a tensor, there are constraints on the form of the tensor that follow from the symmetry of the underlying material. We will discuss this constraint, called Neumann's Principle, in a later lecture.
Models for Diamagnetic and Paramagnetic Anisotropic Materials
Because the equations for magnetization and polarization are so similar, it is not surprising that the anisotropic material properties will have a similar form.
The general (anisotropic) relationship between the induced magnetization density and the applied field is
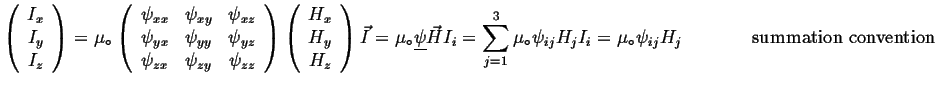 |
(07-8) |
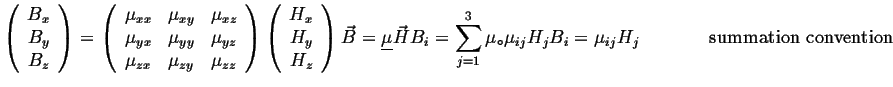 |
(07-9) |
Models for Anisotropic Elastic Materials: Advanced Material
An elastic material is one that responds to an applied stress by deforming--and then ``pops'' back to its original shape when the stress is returned to its original value.
The resistance to deformation--or material stiffness--is ultimately related to the bonds between the atoms or molecules that comprise a solid. Weak bonds in a particular direction would result in a material that is not very stiff--in other words, highly compliant--when a force is applied in the direction of the weak bonds.
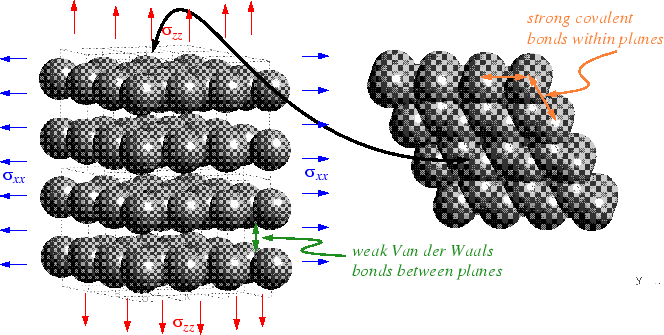 |
Because the stress is a rank-2 tensor (i.e., it has two components
![]() and
and
![]() ) and
the strain
) and
the strain
![]() is also a rank-2 tensor, the most general linear relationship between
the two is:
is also a rank-2 tensor, the most general linear relationship between
the two is:
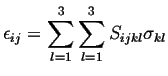 |
(07-10) |
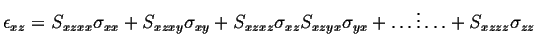 |
(07-11) |