 |
Last time
Elastic Energy Contribution to Coherent Nucleation
 |
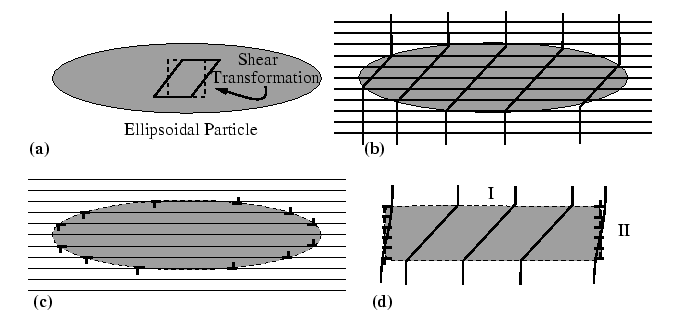
Eshelby Cycle
Shape and Elastic Heterogeneity
Homogeneous Nucleation
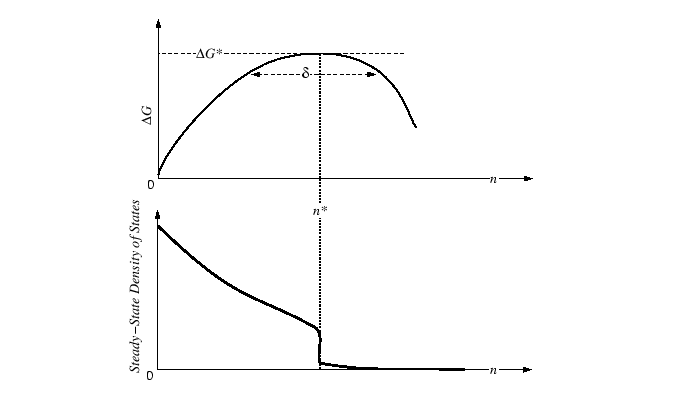 |
Heterogeneous Nucleation
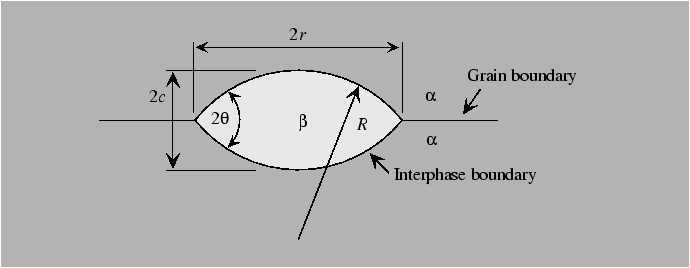
Heterogeneous nucleation can occur on imperfections when the nucleating particle effectively ``replaces'' some energetic feature of the original configuration. For instance, nucleation on a grain boundary removes grain boundary area and replaces it with interphase boundary area that would have been created anyway by formation of the new phase. Thus, preexisting imperfections effectively ``catalyze'' the nucleation process.
 |
Heterogeneous nucleation is a commonly observed phenomenon.
Question: How do you explain the following phenomena?
Heterogeneous nucleation can be understood by considerations of the geometry of
the nucleus.
The steps can be illustrated by a simple example of a cubic crystal with
![]() -facets nucleating in a
-facets nucleating in a ![]() -direction.
-direction.
 |
For this case, the ![]() for homogeneous nucleation is given by the maximum of
for homogeneous nucleation is given by the maximum of
| (32-1) |
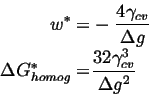 |
(32-2) |
For heterogeneous nucleation,
| (32-3) |
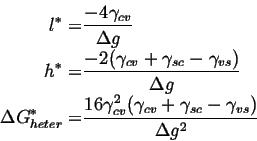 |
(32-4) |
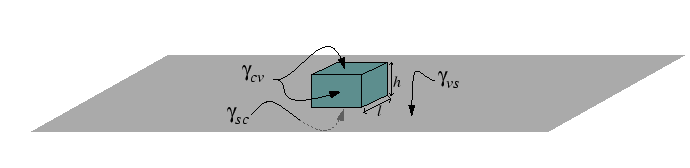
The shape of the particle is determined by the differences in surface tensions and the geometrical factors associated with the shape of the particle determine the nucleation barrier for heterogeneous diffusion.
Spinodal Decomposition and Order-Disorder Transformation Kinetics
Background
The nucleation conditions for phase transformations have been discussed. The rest of this lecture will review another type of initiation mechanism that does not involve nucleation. These mechanisms can either be accompanied by mass flux as in the case of spinodal decomposition or without large-range mass flux as in the case of order-disorder transitions.
These nucleation-free transitions occur when a small local change in the system is never accompanied by an increase in free energy, but always a decrease in free energy.
Spinodal decomposition arises from free energy diagrams and phase diagrams like those illustrated below:
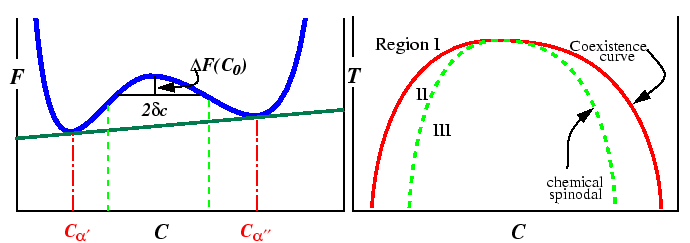 |
In order-disorder transitions such as a ferromagnetic transition or a lattice-ordering, there are no conserved quantities which would give rise to a common tangent in the above diagram.
The two different kinds of processes can be illustrated schematically:
The ordering reaction does not require long-range diffusion, but the decomposition reaction must move mass over long distances.
In the appendix to these notes, it is demonstrated how the changes in free energy depend on whether flux is required or not. The important results can be summarized as follows:
Therefore, an order parameter can always decrease the free energy
by picking a variation
![]() with a sign that makes the product in
Eq. 32-24 negative.
An non-conserved order parameter has no barrier against reaching a
value which makes the free energy a local minimum.
with a sign that makes the product in
Eq. 32-24 negative.
An non-conserved order parameter has no barrier against reaching a
value which makes the free energy a local minimum.
In fact, it can be shown that the sign of the diffusivity, ![]() , for
concentration flux is given by the second derivative
, for
concentration flux is given by the second derivative
![]() .
This has the effect of causing ``up-hill'' diffusion.
.
This has the effect of causing ``up-hill'' diffusion.
Macroscopic Theories for Decomposition Kinetics
If transformations occur without nucleation, then the thermodynamics must account for continuous variations of thermodynamic state variables. These continuous variations are called ``diffuse interfaces'' and they are addressed in this section. The important result is that the local free energy density has a contribution due to gradients of thermodynamic state variables.
The theory for the free energy of inhomogeneous systems was developed by
Cahn and Hilliard in 1958.
The theory was originally developed to account for contributions to
the free energy from gradients in the composition--or any other
conserved field.
The diffuse interface method was extended to non-conserved order parameters
by Allen and Cahn (1979) in their study of the kinetics of
the order-disorder transition.
The theories for both can be developed in parallel since their construction
follows from the same principles.
![]() describes any conserved field quantity
(like the concentration field in a closed system) and
describes any conserved field quantity
(like the concentration field in a closed system) and
![]() represents any non-conserved order parameter field.
represents any non-conserved order parameter field.
A two-phase system with a miscibility gap at equilibrium with a
planar interface will have an
equilibrium composition profile ![]() through the interfacial region.
The form of the equilibrium composition distribution is determined
by the
through the interfacial region.
The form of the equilibrium composition distribution is determined
by the ![]() which minimizes
which minimizes ![]() ,
the total free energy of the system.
Similarly, a system that tends to form long-range ordered domains will
have a distribution of order,
,
the total free energy of the system.
Similarly, a system that tends to form long-range ordered domains will
have a distribution of order, ![]() , across a
planar interface between two identical domains having
different local minima in their order parameters.
, across a
planar interface between two identical domains having
different local minima in their order parameters.
Example profiles, ![]() and
and ![]() , through diffuse interfaces
in these two types of systems
are shown schematically below:
, through diffuse interfaces
in these two types of systems
are shown schematically below:
The profiles ![]() and
and ![]() are continuous and
the compositions
are continuous and
the compositions
![]() and
and
![]() are the
equilibrium compositions of the bulk phases.
The values of order parameter
are the
equilibrium compositions of the bulk phases.
The values of order parameter ![]() and
and ![]() correspond to
local minima in the free energy.
correspond to
local minima in the free energy.
Let ![]() stand for either
stand for either ![]() or
or ![]() .
Also, let
.
Also, let
![]() be the free energy of a small volume
be the free energy of a small volume ![]() which has average composition
which has average composition ![]() and a gradient
and a gradient ![]() across it.
If the free energy density is expanded about its homogeneous value
across it.
If the free energy density is expanded about its homogeneous value
![]() (presumably a known function) then
then
(presumably a known function) then
then
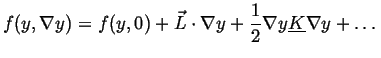 |
(32-7) |
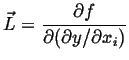 |
(32-8) |
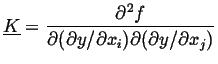 |
(32-9) |
If homogeneous material has a center of symmetry, the free energy
cannot depend on the direction of the gradient and thus
![]() and
and
![]() will be a symmetric matrix.
Furthermore, if the homogeneous material is isotropic (or cubic),
then
will be a symmetric matrix.
Furthermore, if the homogeneous material is isotropic (or cubic),
then
![]() will be a diagonal matrix (with components
will be a diagonal matrix (with components ![]() along the
diagonal), then
free energy density is, to second order:
along the
diagonal), then
free energy density is, to second order:
Only the second term
contributes to the free energy only in the region near the interface
(where the gradient is non-zero).
The gradient-energy coefficient ![]() is a parameter which
contributes to the interfacial area. However, it is not the
only term which contributes: as the composition profile
traverses the interface region,
compositions from the non-equilibrium parts of the free energy curve
are contributing to the excess free energy
associated with the interface as well.
is a parameter which
contributes to the interfacial area. However, it is not the
only term which contributes: as the composition profile
traverses the interface region,
compositions from the non-equilibrium parts of the free energy curve
are contributing to the excess free energy
associated with the interface as well.
It is possible to calculate equilibrium profiles in terms of the
parameters in Eq. 32-10.
However, our purpose is describe the kinetics of how
an arbitrary distribution
![]() evolves towards equilibrium.
evolves towards equilibrium.
We will take a variational calculus approach. The treatment below assumes no prior knowledge of the calculus of variations and will serve as an introduction to the subject.
The total free energy of the entire system (occupying the domain ![]() ) is:
) is:
If the field
![]() is changing with
velocity
is changing with
velocity
![]() , the is the rate of change of
, the is the rate of change of ![]() is
is
![$\displaystyle \frac{\partial F}{\partial t} \ensuremath{\left.\mbox{\rule{0pt}{16pt}}\right\vert}_{t=0} = \int_\Omega [ f'(y) v + K \nabla y \cdot \nabla v ] dV$](img61.gif) |
(32-13) |
| (32-14) |
The change in total energy in Eq. 32-15 is the sum of local
variations:
![]() .
Therefore, the largest possible increase of
.
Therefore, the largest possible increase of ![]() is when the flow,
is when the flow,
![]() , is proportional to
, is proportional to
The functional gradient is the starting point for the kinetic equations for conserved and non-conserved parameter fields.
Appendix: Free Energy Changes and Geometric Constructions
The free energy versus composition curve, illustrated in the
above for a constant temperature,
is a familiar example of a free energy which
gives rise to a miscibility gap.
The region between the spinodal lines delimits those compositions for
which there is no barrier to decomposition.
Inside the miscibility gaps, but outside of the spinodal region, decomposition
is favored but a thermodynamic barrier requires large fluctuations in
composition (i.e., nucleation) for decomposition.
The position of spinodal lines is determined
by the sign of the free energy change for a small fluctuation in composition.
The following derivation is from Hilliard which derives
the variation of the molar free energy,
![]() ,
but this derivation applies
to any extensive molar quantity.5.
,
but this derivation applies
to any extensive molar quantity.5.
We can write
![]() in terms of its partial molar quantities,
in terms of its partial molar quantities,
![]() and
and
![]() :
:
 |
(32-17) |
| (32-18) |
 |
However, if the system is closed (which is the
case for a localized fluctuation in composition), then it is necessary to
account for the exchange of material necessary to satisfy the constraint
of fixed composition.
For each mole transformed, the change in
![]() for the
for the ![]() moles
of the
moles
of the ![]() component is
component is
![]() , with a
similar term for the
, with a
similar term for the ![]() component:
component:
| (32-19) |
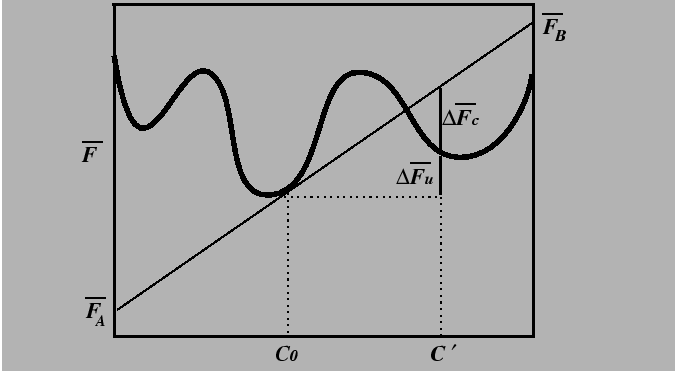
![\begin{displaymath}\begin{array}{ll} \Delta \overline{F} = & c' \overline{F}_B(c...
... - c') [ \overline{F}_B(c_0) - \overline{F}_A(c_0)] \end{array}\end{displaymath}](img90.gif) |
(32-20) |
Consider the special case of a small composition fluctuation,
![]() .
Expanding
.
Expanding
![]() in
in ![]() :
:
Substituting Eq. 32-21 into Eq. 32-22 results in the
change in the molar free energy for a variation of a conserved
parameter ![]() :
:
Similarly, the lowest order term for the
change in the molar free energy for a variation of a non-conserved
order parameter ![]() is
is
Therefore, an order parameter can always decrease the free energy
by picking a variation
![]() with a sign that makes the product in
Eq. 32-24 negative.
An non-conserved order parameter has no barrier against reaching a
value which makes the free energy a local minimum.
with a sign that makes the product in
Eq. 32-24 negative.
An non-conserved order parameter has no barrier against reaching a
value which makes the free energy a local minimum.
On the other hand, for a conserved quantity like ![]() , the variation
in molar free energy is proportional to
, the variation
in molar free energy is proportional to
![]() .
Therefore, a barrier to the growth of small variations exists whenever
the second derivative in Eq. 32-23 is positive.
Thus, nucleation is required for a transformation outside of the
spinodal curves.
.
Therefore, a barrier to the growth of small variations exists whenever
the second derivative in Eq. 32-23 is positive.
Thus, nucleation is required for a transformation outside of the
spinodal curves.
The sign of Eq. 32-23
determines the sign of the interdiffusion coefficient.