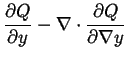- ...
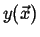 1
1
- A functional is a function of a function;
in this case, it takes a function and maps it to a scalar
which is numerically equal to the total free energy of the system
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
values2
- If
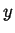 represents a conserved quantity like
represents a conserved quantity like 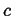 , then
the variation
, then
the variation 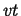 must not contribute to the total content of the
system (
must not contribute to the total content of the
system (
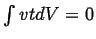 ), but we will satisfy this requirement
automatically below.
), but we will satisfy this requirement
automatically below.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....3
-
This is one particular choice for the functional gradient,
for which there
are an infinite number of choices.
This particular choice (the gradient in the
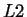 -norm
of functions) describes the physics of the problem.
-norm
of functions) describes the physics of the problem.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....4
-
For the general functional,
![$ P[y] = \int Q[y(\vec{x}),\nabla y] dV$](img71.gif) ,
the variational derivative of
,
the variational derivative of 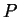 is
is
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... quantity.5
-
An extensive quantity is one which depend on the total size of a system,
like the volume, enthalpy, or free energy.
A molar extensive quantity is scaled by diving by the total number of
moles in the system:
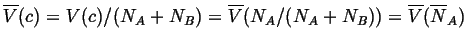 .
A molal extensive quantity is scaled by dividing by the number of
moles of a particular species.
.
A molal extensive quantity is scaled by dividing by the number of
moles of a particular species.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.