Last time
Diffuse Interface Approximation
Functional Gradient
Kinetics for Non-conserved Order Parameters
Kinetics for Conserved Order Parameters
Nucleation
The transformation of a metastable material by the growth of initially small fluctuations (e.g., composition fluctuations in the case of spinodal decomposition) was treated as a continuous transformation.
Some metastable systems are stable with respect to infinitesimal fluctuations, but are unstable to a perturbation in the form of a finite fluctuation. In such systems, the transformation does not proceed until a finite fluctuation occurs. If the necessary fluctuation is so large that its probability of it occurring in any observable time is effectively zero, then the system is kinetically `frozen' in its metastable state. Many, if not most, engineering materials are in such non-equilibrium states.
Each of these finite fluctuations is called a nucleus; the metastable medium is called the matrix. The minimum size nucleus required for continued spontaneous growth is called a critical nucleus and all the fluctuations smaller than the critical nucleus are called sub-critical nuclei. The process by which the sub-critical nuclei change their size by the (energetically favorable) loss of its atoms to the matrix and the improbable attachment of new matrix atoms onto the sub-critical nucleus is called nucleation.
Nucleation is commonly observed in carbonated beverages.
When a beverage
container is capped, the amount of dissolved
CO![]() that is in equilibrium at capped pressure is greater than
the amount of dissolved
CO
that is in equilibrium at capped pressure is greater than
the amount of dissolved
CO![]() in equilibrium at atmospheric pressure.
The bubbles of
CO
in equilibrium at atmospheric pressure.
The bubbles of
CO![]() that form in an opened beverage and float to
the top are the result of nucleation process.
that form in an opened beverage and float to
the top are the result of nucleation process.
Common experience also demonstrates that there are two different categories of nucleation. The nucleation of critical nuclei at defects such as surface imperfections is called heterogeneous nucleation; nucleation that occurs randomly throughout the volume of the metastable matrix is homogeneous nucleation.
Nucleation Regimes
Nucleation is what precedes growth by phase transformation.
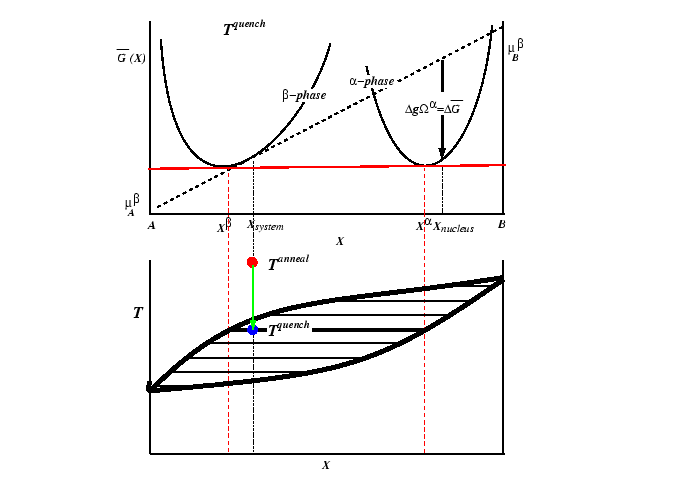
Consider the case of a solid solution of phase ![]() at a
composition that is metastable with respect to the creation
of an
at a
composition that is metastable with respect to the creation
of an ![]() -phase.1
-phase.1
A prototypical case can be illustrated with a phase diagram and free energy curve.
 |
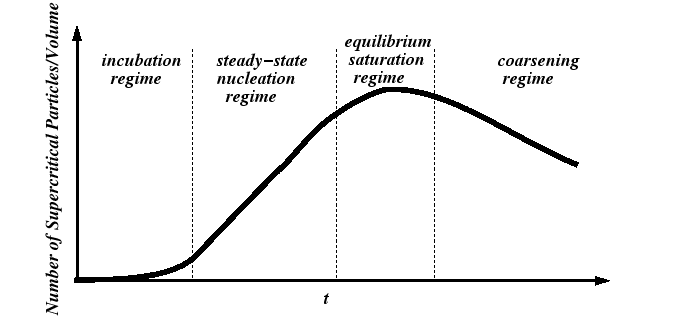
A useful theory of nucleation should predict at least two quantities:
These quantities are related to the so-called nucleation regimes:
 |
Homogeneous Nucleation: Simple Theory
It is possible to formulate a very simple theory for the size of
a critical nucleus from macroscopic thermodynamic quantities:
interfacial surface tension
![]() (energy/area), and free energy
change per unit volume nucleus
(energy/area), and free energy
change per unit volume nucleus ![]() (energy/volume).
This simple theory works remarkably well despite the
fact that, at the small sizes that critical nuclei are formed
(10-50Å),
extrapolation of
(energy/volume).
This simple theory works remarkably well despite the
fact that, at the small sizes that critical nuclei are formed
(10-50Å),
extrapolation of
![]() and
and ![]() is questionable.
Another advantage is that the model provides a useful understanding of the
physical quantities that control nucleation.
is questionable.
Another advantage is that the model provides a useful understanding of the
physical quantities that control nucleation.
An ![]() -phase nucleus forming in a
-phase nucleus forming in a ![]() -matrix has
only two contributions to its energy: the decrease in energy
due to the volumetric driving force,
-matrix has
only two contributions to its energy: the decrease in energy
due to the volumetric driving force, ![]() , and an increase in
energy due to surface tension,
, and an increase in
energy due to surface tension,
![]() .2
.2
For a spherical isotropic nucleus of radius ![]() , the total free energy is:
, the total free energy is:
Suppose nuclei are formed by random fluctuations and a distribution ![]() of
nuclei sizes
of
nuclei sizes ![]() develops.
Any one of the nuclei having a radius
develops.
Any one of the nuclei having a radius ![]() such that
such that
![]() can decrease its free energy continously by growing (i.e., increasing
its radius); all other nuclei cannot grow
continuously, but may grow by improbable events such as random attachment of
add-atoms.
Thus, the size of the critical nucleus must satisfy
can decrease its free energy continously by growing (i.e., increasing
its radius); all other nuclei cannot grow
continuously, but may grow by improbable events such as random attachment of
add-atoms.
Thus, the size of the critical nucleus must satisfy
![]() ;
it is the radius that maximizes
;
it is the radius that maximizes
![]() 3
3
The growth of subcritical nuclei increases the nucleus free energy with
each increment of nucleus size.
The process will be treated as a sequence of activated states similar to
the activation process for a vacancy exchange as described in
Chapter 6 of KPIM.
Assuming that the nucleation occurs at constant pressure and temperature, the
nuclei sizes will be distributed with a probability proportional to
![]() where
where
![]() is the total free energy of a nucleus containing
is the total free energy of a nucleus containing ![]() atoms.
Equation 24-2 can be converted using
atoms.
Equation 24-2 can be converted using
![]() to
to
A Model for the Steady-State Nucleation Rate
A subcritical nucleus has a driving force which tends to make it shrink and
dissolve back into the matrix.
The development and incremental growth of subcritical nuclei is assumed to
be a thermally activated process.
The steady-state nucleation regime subsists by the development of a steady-state
size distribution of subcritical clusters.
At steady-state, the source of the material to produce subcritical
clusters is sufficient to replenish the material that is lost as
a critical cluster becomes a stable precipitate and grows.
The rate at which subcritical clusters reach their critical size
must be the steady-state nucleation rate,
![]() and
can be experimentally determined from the slope in Fig. 24-2.
and
can be experimentally determined from the slope in Fig. 24-2.
The steady-state nucleation rate depends on the distribution of subcritical nuclei.
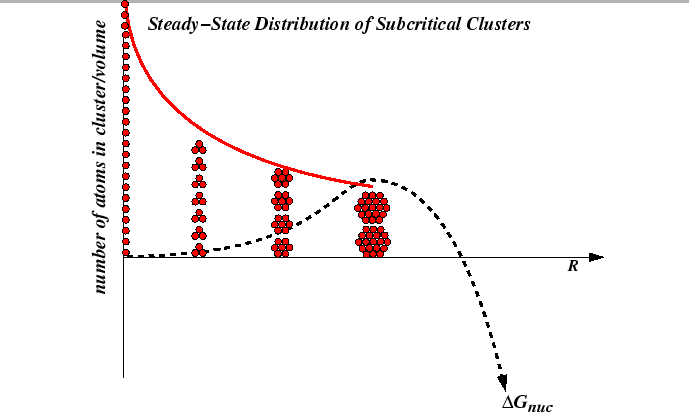 |
The rate of creation of critical nuclei can be extended to
subcritical nuclei as follows.
The rate at which subcritical nucleus of size ![]() (per unit volume) are created must
must be related to the concentration of nuclei of size
(per unit volume) are created must
must be related to the concentration of nuclei of size ![]() that
grow by one unit minus the rate at which those of size
that
grow by one unit minus the rate at which those of size ![]() lose
one unit:
lose
one unit:
We assume that there is a steady-state distribution for which the ``flux'' ![]() must vanish, so4
must vanish, so4
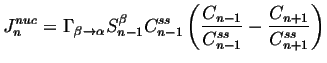 |
(24-6) |
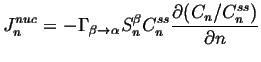 |
(24-7) |
Therefore the rate of change of the concentration of nuclei of size ![]() must
be related to the divergence of this flux:
must
be related to the divergence of this flux:
At steady-state,
![]() can be integrated with
respect to
can be integrated with
respect to ![]() .
The integration constant must be
.
The integration constant must be
![]() and not a function of
and not a function of ![]() :
:
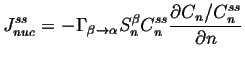 |
(24-9) |
which can be integrated again from one particle (where it may be
assumed that
![]() ) to an infinite number of
particles where
) to an infinite number of
particles where
![]() as
as
![]() .
.
Several approximations must be made to replace the first integral in Eq. 24-10
with simple forms.
The integrand over ![]() is large only when
is large only when
![]() , which is small near
, which is small near
![]() --so the
limits of integration can be extended to
--so the
limits of integration can be extended to
![]() without addition
of significant error.
The thermally activated concentration
without addition
of significant error.
The thermally activated concentration
![]() where
where ![]() is the number of possible homogeneous nucleation sites per volume
and the nucleation barrier can be expanded around the critical size:
is the number of possible homogeneous nucleation sites per volume
and the nucleation barrier can be expanded around the critical size:
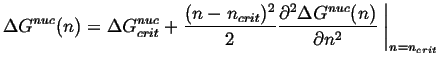 |
(24-11) |
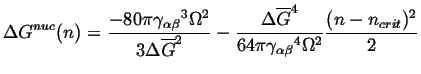 |
(24-12) |
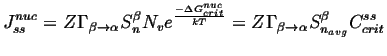 |
(24-13) |
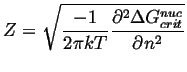 |
(24-14) |
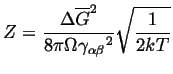 |
(24-15) |
Typical experimental values of
![]() .
.
Model for the Nucleation Incubation Time
Considerations of thermally activated subcritical nuclei resulted
in a diffusion equation for the rate of change of the density of
nuclei of size ![]() in Eq. 24-8 with an effective
diffusivity given by
in Eq. 24-8 with an effective
diffusivity given by
![]() .
.
The incubation time is approximately the amount of time before particles begin reaching the critical size. The nucleation and growth process throughout all regimes implies that the particle size distribution is changing over time:
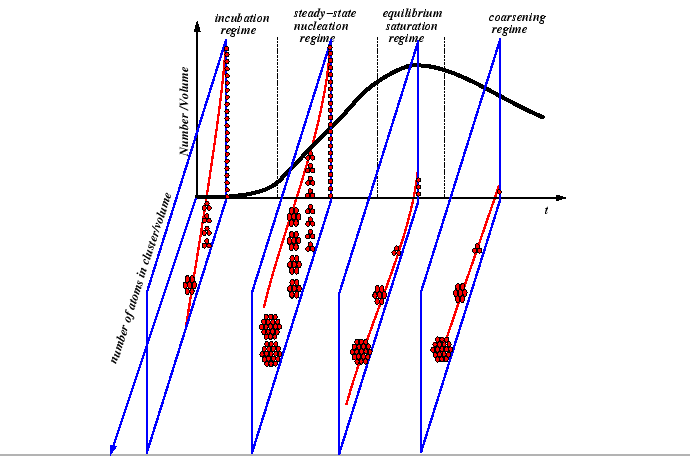 |
This diffusion equation could be solved for
an initial distribution of clusters with a fixed
concentration at small sizes (![]() ) and zero flux
at
) and zero flux
at ![]() to yield a characteristic time when
appreciable concentrations appear at
to yield a characteristic time when
appreciable concentrations appear at
![]() .
.
However, the incubation time can be approximated
with a random walk model as follows.
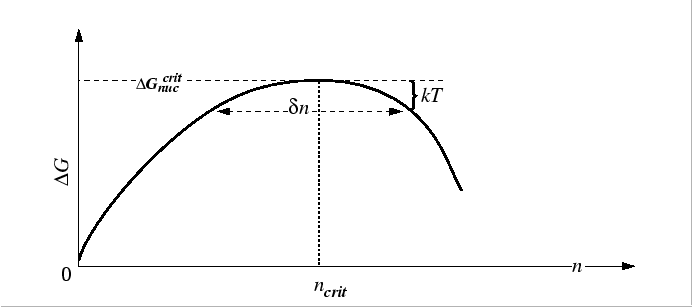
Near
![]() ,
,
![]() is nearly flat
and the rate of the number of particles crossing
is nearly flat
and the rate of the number of particles crossing
![]() can be approximated by the root-mean-square `displacement'
relation for a one-dimensional random walk:
can be approximated by the root-mean-square `displacement'
relation for a one-dimensional random walk:
![]() where
where
![]() is the `distance' on either side of the maximum that
is the `distance' on either side of the maximum that
![]() can be considered to be flat.
Approximating the
can be considered to be flat.
Approximating the
![]() by the value at which
by the value at which
![]() ,
,
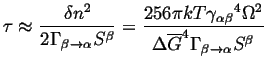 |
(24-16) |
 |