Next: About this document ...
![]()
![]()
![]()
Next: About this document
...
Last time
Order Parameters
Continuous and Discontinuous Transformations
Free Energy Changes for Conserved and Non-conserved Order Parameters
Free Energy Density and Diffuse Interfaces
Continuous Phase Transformations--Kinetics
The functional gradient is the starting point for the kinetic equations for conserved and non-conserved parameter fields. From an integral over the homogeneous free energy density and a gradient energy term:
![$\displaystyle F[y(x)] = \int_\Omega ( f(y) + \frac{K}{2} \nabla y \cdot \nabla y) dV$](img1.gif) |
(23-1) |
This is the free energy for a domain ![]() for an arbitrary field
for an arbitrary field ![]() representing an order parameter.
representing an order parameter.
Supposing the the order parameter field is changing (or, flowing) with
velocity field ![]() ,
the free energy as a function of time is
,
the free energy as a function of time is ![]() and the instantaneous rate of total free energy change:
and the instantaneous rate of total free energy change:
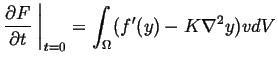 |
(23-2) |
from this equation, it follows that the fastest1decrease
in total free energy if the flow field ![]() is chosen so that it is `parallel' to (minus) the functional gradient
is chosen so that it is `parallel' to (minus) the functional gradient
![]() which is defined by:
which is defined by:
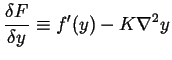 |
(23-3) |
Kinetics of Non-conserved Order Parameters:
The Allen-Cahn Equation
For a non-conserved order parameter ![]() ,
Eq.
,
Eq. ![]() is the local rate of increase of free energy for a small change
is the local rate of increase of free energy for a small change
![]() ;
therefore
;
therefore ![]() is the driving force to change
is the driving force to change ![]() .
No long-range diffusion is required (in other words, the order
parameter can change with no flux of order into an element
.
No long-range diffusion is required (in other words, the order
parameter can change with no flux of order into an element ![]() ).
Therefore, assuming kinetics that are linear in the driving force:
).
Therefore, assuming kinetics that are linear in the driving force:
![$\displaystyle \frac{\partial \eta}{\partial t} = M_\eta [K_\eta \nabla^2 \eta - f'(\eta)]$](img14.gif) |
(23-4) |
which is known as the Allen-Cahn equation for describing order-disorder kinetics. It is also called Model A or the non-conserved Ginsberg-Landau equation.
Allen-Cahn: Critical Microstructural Wavelengths
Consider a system where ![]() has two minima at
has two minima at ![]() :
:
| (23-5) |
where ![]() is the height at the unstable saddle point at
is the height at the unstable saddle point at ![]() .
Suppose the system is initially uniform at unstable point
.
Suppose the system is initially uniform at unstable point ![]() (for instance, the system may have been quenched from a higher
temperature, disordered state and
(for instance, the system may have been quenched from a higher
temperature, disordered state and ![]() represent two equivalent ordering variants). If the system is
perturbed a small amount by a planar perturbation in the
represent two equivalent ordering variants). If the system is
perturbed a small amount by a planar perturbation in the ![]() -direction,
-direction,
![]() .
Putting this and Eq. 23-5
into Eq. 23-4, and
keeping the lowest order terms in
.
Putting this and Eq. 23-5
into Eq. 23-4, and
keeping the lowest order terms in ![]() :
:
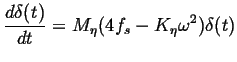 |
(23-6) |
so that
| (23-7) |
The perturbations grow if
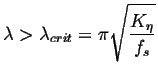 |
(23-8) |
which is approximately equal to the interface width.
Note that the amplification factor is a weakly increasing function of
wavelength (asymptotically approaching ![]() at long wavelengths). This would predict that the longest wavelengths
would dominate the morphology of an order-disorder phase transition.
However, the probability of finding a long wavelength perturbation is a
decreasing function of wavelength and this also has an effect on
morphology.
at long wavelengths). This would predict that the longest wavelengths
would dominate the morphology of an order-disorder phase transition.
However, the probability of finding a long wavelength perturbation is a
decreasing function of wavelength and this also has an effect on
morphology.
The Kinetics of Conserved Parameters:
The Cahn-Hilliard Equation
Because ![]() is a (locally) conserved parameter, the flux of
is a (locally) conserved parameter, the flux of ![]() from one volume element to its neighbor will affect the kinetics.
from one volume element to its neighbor will affect the kinetics.
![]() is guaranteed to be conserved if
is guaranteed to be conserved if
![]() is the divergence of a flux.
is the divergence of a flux.
Equation ![]() is the local increase of free energy density due to a local addition
is the local increase of free energy density due to a local addition
![]() .
The flux is assumed to be linear in the gradient of Eq.
.
The flux is assumed to be linear in the gradient of Eq. ![]() :
:
| (23-9) |
This is equivalent to the linear assumption in Fick's law. The
proportionality factor ![]() is related to the interdiffusion coefficient. However,
is related to the interdiffusion coefficient. However, ![]() is necessarily positive.
is necessarily positive.
Therefore, the local rate of increase of the composition is given by (minus) the divergence of the flux:
![$\displaystyle \frac{\partial c}{\partial t} = \nabla \cdot M_c \nabla [ f'(c(\vec{x})) - K_c \nabla^2 c(\vec{x})]$](img34.gif) |
(23-10) |
if ![]() is constant, then
is constant, then
![$\displaystyle \frac{\partial c}{\partial t} = M_c [\nabla^2 f'(c(\vec{x})) - K_c \nabla^4 c(\vec{x})]$](img35.gif) |
(23-11) |
which is known as the Cahn-Hilliard equation describing the kinetics of spinodal decomposition. It is also called Model B or the conserved Ginsberg-Landau equation.
The first term on the right-hand side of Eq. 23-11 looks like the
classical diffusion equation in regions where ![]() can be reasonably approximated by a quadratic function, (for instance
near the minima of
can be reasonably approximated by a quadratic function, (for instance
near the minima of ![]() ).
The fourth-order term has the effect of stabilizing the shortest
wavelengths when
).
The fourth-order term has the effect of stabilizing the shortest
wavelengths when ![]() ,
as discussed below.
,
as discussed below.
Cahn-Hilliard: Critical and Kinetic Wavelengths
Consider the following function as an approximation to the regular solution model:
![$\displaystyle f(c) = \frac{16 f_s}{(c_\beta - c_\alpha)^4} [ (c - c_\alpha)(c - c_\beta) ]^2$](img39.gif) |
(23-12) |
which has minima at concentrations ![]() and
and ![]() and a maximum of height
and a maximum of height ![]() at
at ![]() .
Suppose we have an initially uniform solution at
.
Suppose we have an initially uniform solution at
![]() and that we perturb the concentration with a small plane wave:
and that we perturb the concentration with a small plane wave:
![]() .
Putting this into Eq. 23-11
and keeping the lowest-order terms in
.
Putting this into Eq. 23-11
and keeping the lowest-order terms in ![]() ,
,
![$\displaystyle \frac{d \epsilon}{dt} = \frac{M_c \omega^2}{(c_\beta - c_\alpha)^2} [16 f_s - K_c \omega^2(c_\beta - c_\alpha)^2] \epsilon$](img46.gif) |
(23-13) |
Therefore any wavelength ![]() will grow if
will grow if
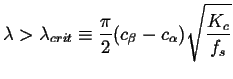 |
(23-14) |
Taking the derivative of the amplification factor in Eq. 23-13 with respect to ![]() and setting it equal to zero, we find the fastest growing wavelength:
and setting it equal to zero, we find the fastest growing wavelength:
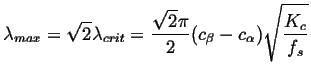 |
(23-15) |
It is expected that domain size in the early stage of spinodal
decomposition will be approximately ![]() .
.
Note that this approach for conserved order parameter is analogous to the case of kinetic and thermodynamic stability of a cylinder with axial perturbations:
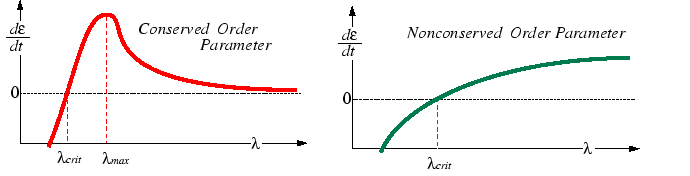 |
Simulations
Below are simulations of Eqs. 23-4 and 23-11 with initial conditions taken as a small perturbation about the unstable (or saddle) point.
Can you determine, by observation, which simulation corresponds to which type of kinetics?
 |
 |
![]()
![]()
![]()
Next: About this document
...