The Successful Jump Frequency as an Activated Process
Energy Distributed among Particles in an Ensemble of Fixed Energy
The Square Well Approximation
The Harmonic Well Approximation
Many-Body Theory of Activated Processes at Constant Pressure
In a real system, an atom or a vacancy does not make a
successful hop without affecting (or getting effected by) its
neighbors--all of the particles are vibrating and saddle point
energy is an oscillating target produced by the random vibrations
of all the atoms.
The
energy-surface that an atom, interstitial, or vacancy travels upon
is a complicated and changing surface.
If there are ![]() spherical particles, then there are
spherical particles, then there are ![]() -degrees
of freedom to this surface, but it will be assumed that the momentum
variables can be averaged out so that only a
-degrees
of freedom to this surface, but it will be assumed that the momentum
variables can be averaged out so that only a ![]() -dimensional
potential surface remains:
-dimensional
potential surface remains:
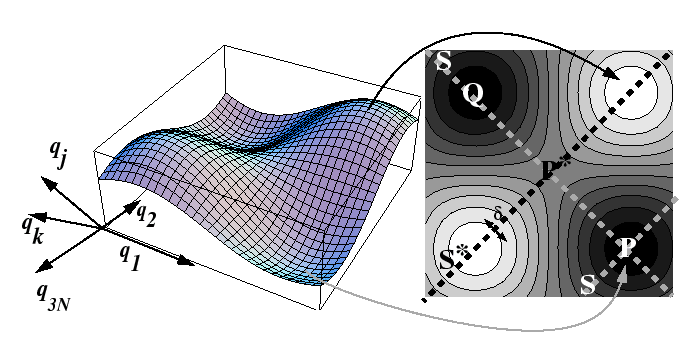 |
Effectively, the average over the momentum variables is supposed to account for events such as increased probability of a hop by an interstitial or vacancy when the oscillations of nearby host atoms cooperate to create an enlarged path (or reduced activation barrier).
The minima, or equilibrium values of momenta and positions, can be approximated by harmonic wells:
Considering the process of a single hop, consider the trajectory
of the particle as illustrated in Figure 15-1.
It can be supposed that trajectory
![]() is along
the positive direction of the coordinate
is along
the positive direction of the coordinate ![]() .
This effectively turns the many-body problem into a one-dimensional
problem along the line
.
This effectively turns the many-body problem into a one-dimensional
problem along the line ![]() in Figure 15-1.
Therefore, the rate of crossing can be related to the average velocity
in the activated state and the ``effective width'' in the activated state.1
in Figure 15-1.
Therefore, the rate of crossing can be related to the average velocity
in the activated state and the ``effective width'' in the activated state.1
Let the first coordinate be in the direction of the crossing
(parallel to ![]() ), then the average
(rms) momentum
), then the average
(rms) momentum ![]() in that direction is related to the an average rate
of attempts.
The result that was derived
for the harmonic potential can be re-used in this case:
in that direction is related to the an average rate
of attempts.
The result that was derived
for the harmonic potential can be re-used in this case:
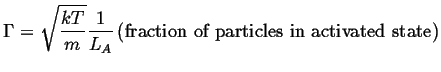 |
(15-2) |
However, in this case, the particle may have a different volume in the activated state compared to the equilibrium state:2
| (15-3) |
For the case where the volume may vary, but pressure is constant, the canonical constant pressure partition function must be used:
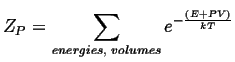 |
(15-4) |
Therefore
![]() picks up an additional factor:
picks up an additional factor:
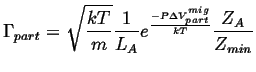 |
(15-5) |
It remains to evaluate the partition functions by summing
over all energies:
![]() .
The usual strategy in evaluating the sum for a partition
function is to replace it with an integration over
a continuous variable:
.
The usual strategy in evaluating the sum for a partition
function is to replace it with an integration over
a continuous variable:
![]() ,
where
,
where ![]() is a continuous variable that mimics the index
is a continuous variable that mimics the index ![]() .
However, because the atoms are part of a lattice, the
positions and momenta are quantized.
Therefore, a trick must be employed to convert the
sum over quantized values to continuous values.
The trick involves degeneracy and the Heisenberg uncertainty
principle.
The partition function is evaluated by passing to the classical limit
by dividing up the quantum phase space into cells of side-length equal
to Planck's constant,
.
However, because the atoms are part of a lattice, the
positions and momenta are quantized.
Therefore, a trick must be employed to convert the
sum over quantized values to continuous values.
The trick involves degeneracy and the Heisenberg uncertainty
principle.
The partition function is evaluated by passing to the classical limit
by dividing up the quantum phase space into cells of side-length equal
to Planck's constant, ![]() :
:
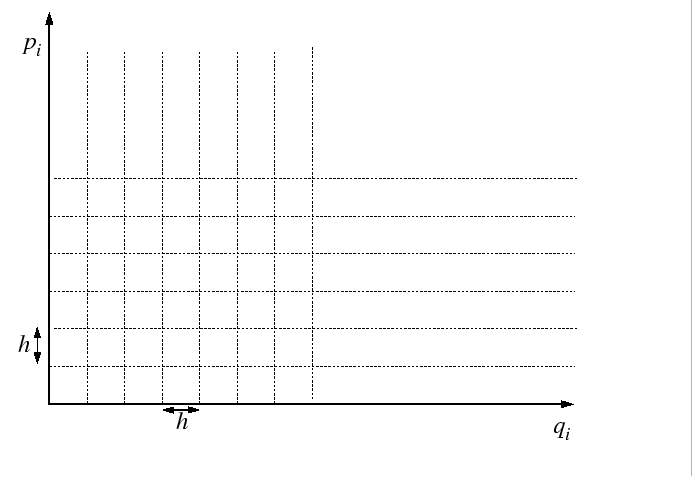 |
Because of the uncertainty principle:
| (15-6) |
Each elementary volume,
![]() ,
in phase space must be considered to have degeneracy:
,
in phase space must be considered to have degeneracy:
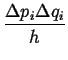 |
(15-7) |
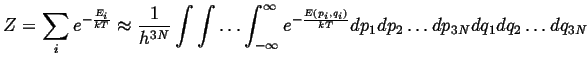 |
(15-8) |
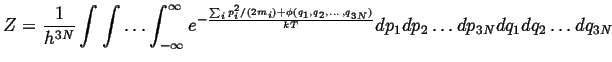 |
(15-9) |
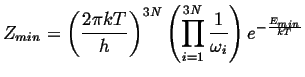 |
(15-10) |
Carrying out the same process for the activated state (which
has one less degree of freedom) except for the momentum ![]() that will have
the slow mode as it traverses the saddle point, there are
that will have
the slow mode as it traverses the saddle point, there are ![]() natural
frequency and one averaged velocity near the saddle point.
natural
frequency and one averaged velocity near the saddle point.
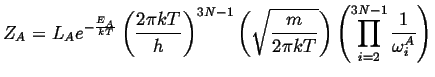 |
(15-11) |
The products over the vibrational modes can be related to the entropies of the states, i.e.,
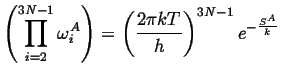 |
(15-12) |
Putting this all back into the expression for the rate of jumps,
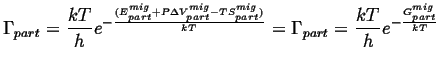 |
(15-13) |
Advanced Topic: Variational Flows
Suppose that the free energy for the entire system can be written as an integral over the local volumes, to simplify the discussion consider one dimension:
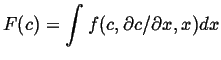 |
(15-14) |
Recall the discussion in the first few lectures about the gradient and
directional derivative.
One might consider if the field ![]() is changing or flowing with
velocity
is changing or flowing with
velocity ![]() , how would this affect the total energy
, how would this affect the total energy ![]() ?
The recipe is:
?
The recipe is:
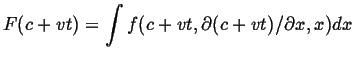 |
(15-15) |
![$\displaystyle \frac{\partial F}{\partial t} \ensuremath{\left.\mbox{\rule{0pt}{...
...{\partial c/\partial x}}}\ensuremath{\frac{\partial{v}}{\partial{x}}}\right] dx$](img53.gif) |
(15-16) |
Integrating by parts4
![$\displaystyle \frac{\partial F}{\partial t} \ensuremath{\left.\mbox{\rule{0pt}{...
...x}}}\ensuremath{\frac{\partial{f}}{\partial{\partial c/\partial x}}}\right]v dx$](img56.gif) |
(15-17) |
![$\displaystyle v \propto - M \left[ \ensuremath{\frac{\partial{f}}{\partial{c}}}...
...ial{x}}}\ensuremath{\frac{\partial{f}}{\partial{\partial c/\partial x}}}\right]$](img57.gif) |
(15-18) |
This is a rule for how to choose the flow so that the free energy deceases as quickly as possible. Consider some examples that apply to diffusion. For a free energy density with a simple minimum:
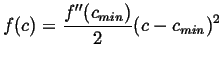 |
(15-19) |
![$\displaystyle J(x,t) = -M \ensuremath{\nabla}\left[ \ensuremath{\frac{\partial{...
...rtial c/\partial x}}}\right] = -M \ensuremath{\nabla}f''(c_{min}) (c - c_{min})$](img59.gif) |
(15-20) |
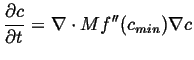 |
(15-21) |
Alternatively, one could consider the local energy density as being composed of the penalty for being inhomogeneous, in this case the local free energy penalty goes like:
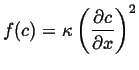 |
(15-22) |
In this case, the gradient is not conserved, so the linear kinetic approximation for the change in concentration field is:
![$\displaystyle \ensuremath{\frac{\partial{c}}{\partial{t}}}= -M \left[ \ensurema...
...ial c/\partial x}}}\right] = M \ensuremath{\frac{\partial^2{c}}{\partial{x}^2}}$](img63.gif) |
(15-23) |