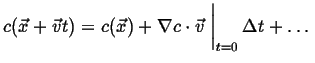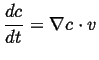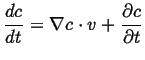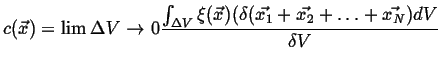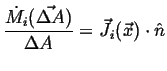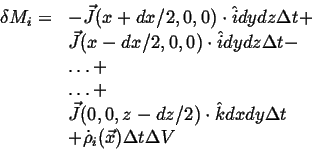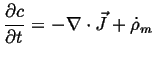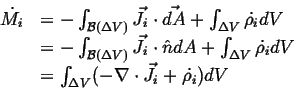Next: About this document ...
3.21 Spring 2002: Lecture 01
- Class Structure (Described in Syllabus)
Lectures will be mostly chalk on the board, supplemented by computer simulations and
graphics.
This is a 15 unit class. You are expected to spend 5 (waking) hours in lectures.
The other ten hours should be occupied by reading the text or any supplementary
materials, reviewing or recopying your lecture notes, and doing your homework.
If you begin spending significantly more than 15 hours a week on this
class, please confer with your classmates.
The groups are designed to reduce the amount of time spent on homework--not to
increase it.
If the the class is generally spending more than 15 hours, let us know so we can adjust.
- Grading
- 2 exams 25%/exam
- Two exams will be in-class during the lecture period.
- Homework 25%
- Class groups will be organized. Each group will turn in a joint homework and
receive a single grade that is recorded for each member of the group.
Everyone in the group receives the same grade.
- Class Participation 25%
- You will receive credit for asking good questions or making good
comments during lectures and recitations--if you state your
name.
You will not receive credit for ``showing off'':
a good question or a comment is one that benefits most of your classmates.
There will be random questions to students during lectures. You
should be prepared to answer simple questions succinctly or say that
you honestly don't know-and call on a friend.
- Lecture Notes will often be found on the web. You can use them any way you wish.
The lecture notes will supplement (and sometimes correct) the textbook.
- The textbook (KPIM) for this course is being printed at CopyTech. You
should be able to buy a copy next week at CopyTech for a very modest price.
You are expected to read the book and understand the concepts that
are covered in the lecture.
Because the book is still in revision, comments/corrections on the book in the form of writing will
be very welcome and will be regarded
as class participation.
- Office hours can be found on the website.
Thermodynamics and Kinetics
- Joule/Kelvin
-
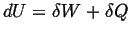 |
(01-1) |
- Carnot/Clausius
- For the limiting case of a reversible process,
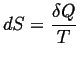 |
(01-2) |
- Boltzmann
-
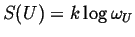 |
(01-3) |
- Gibbs
- Rigorous and mostly complete foundation of
equilibrium of materials.
Two fundamental results.
- If an extensive quantity can be exchanged between two bodies, then
a necessary condition for equilibrium is that the associated potential,
which is an intensive quantity, must have the same value in each body.
- If a system is in equilibrium with reservoir that maintains a
constant potential (e.g.
 and
and 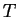 ),
then there exists a free energy function for that system (e.g.,
),
then there exists a free energy function for that system (e.g., 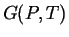 )
that is minimized at equilibrium.
Therefore, a necessary condition for equilibrium is that every small variation
in
)
that is minimized at equilibrium.
Therefore, a necessary condition for equilibrium is that every small variation
in 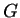 must be non-negative:1
must be non-negative:1
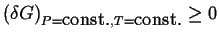 .
.
Figure 1-1:
Representation of all possible values of the molar free energy function that
is minimized at equilibrium.
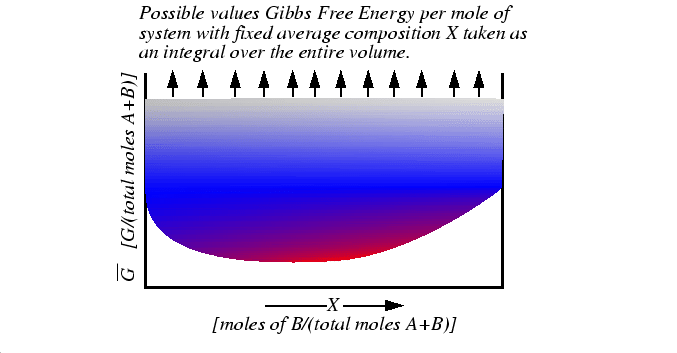 |
The study of materials processes is a combination of Thermodynamics and Kinetics. Kinetics
relies on thermodynamics as a rigorous foundation.
Kinetics is less rigorous and more approximate; but, perhaps applicable to more real systems.
| Materials Processes |
| Relatively few variables |
Complex interations involving a space and time continuum of variables. |
| Precise stratements about equilibrium states or
quasistatic processes |
Approximate statements or models for complex evolving systems |
| Powerful concepts and foundation, but limited to ideal systems |
Approximate but predicitive statements
for a wide range of phenomenae |
Extending Thermodynamics to Kinetics
Figure:
If the two curves on the left represent the
lowest possible values of an appropriate thermodynamic function
function that is minimized at equilibrium (such as
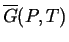 at a fixed value of
at a fixed value of 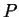 ,
, 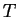 )
and if each phase
constrained to have a homogeneous composition
)
and if each phase
constrained to have a homogeneous composition 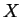 , then these curves are the equilibrium
values of the appropriate free energy as a function of
, then these curves are the equilibrium
values of the appropriate free energy as a function of 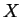 (i.e.,
(i.e.,
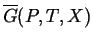 ).
).
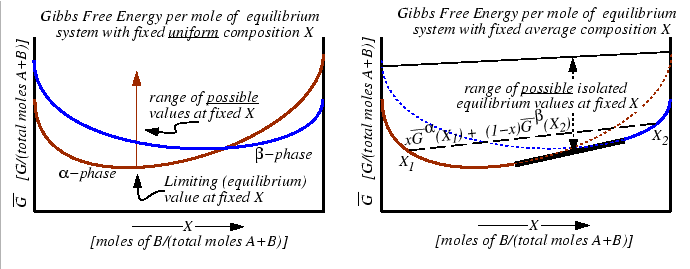 |
If the constraint that the system has a homogeneous composition is removed, then if any
combination of compositions 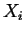 --distributed among all possible phases in such
a way that the average composition is
--distributed among all possible phases in such
a way that the average composition is
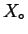 --has a
lower free energy than any homogeneous system, then the equilibrium free energy curve is
the convex hull from below of all the homogenous free energy curves (i.e., the single-phase
compositions of the homogeneous molar free energy curves plus the common tangent).
--has a
lower free energy than any homogeneous system, then the equilibrium free energy curve is
the convex hull from below of all the homogenous free energy curves (i.e., the single-phase
compositions of the homogeneous molar free energy curves plus the common tangent).
The values of `comparison' free energies of systems constructed from linear combinations
of homogeneous equilibrium molar free energies is also bound from above--a set that is
considerably smaller than non-equilibrium values of that function which is minimized during
an approach to equilibrium.
Mathematical Background
- Fields
A field associates a physical quantity with a position,
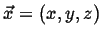 at a time,
at a time, 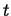 .2A field may also be a function of time:
.2A field may also be a function of time:
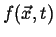 where
where  is the physical quantity that
depends on location and time.
is the physical quantity that
depends on location and time.
- Scalar Fields
-
- Vector Fields
-
- Tensor Fields
-
Figure 1-3:
Two representations of a scalar field in two-dimensions are illustrated
in the left and middle figures.
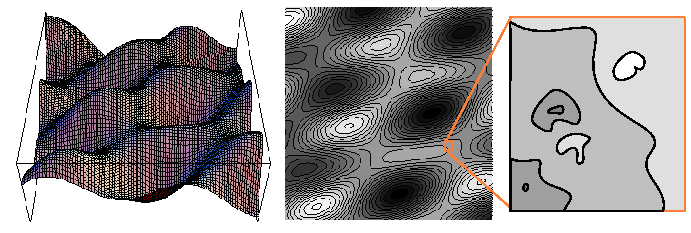 |
Every sufficiently smooth scalar field has a natural vector field
associated with it: the gradient field.
Consider a stationary scalar field
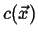 such as the one illustrated
in Figure 1-3.
such as the one illustrated
in Figure 1-3.
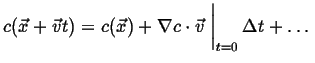 |
(01-4) |
The instantaneous rate of change of 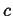 with respect to
with respect to 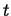 is therefore:
is therefore:
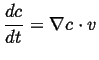 |
(01-5) |
The gradient is parallel to the direction of
steepest ascent.
This can be generalized even further by considering a time-dependent field
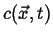 , the instantaneous rate of change of
, the instantaneous rate of change of 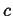 with velocity
with velocity
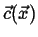 is
is
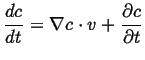 |
(01-6) |
- $&bull#bullet;$
- Continuum Limits
Nature is fundamentally discrete, how is that we can discuss things
like derivates?
Figure 1-4:
Infinitesimal volume with dimensions 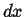 ,
, 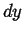 , and
, and 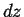 located
at
located
at
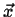 .
.
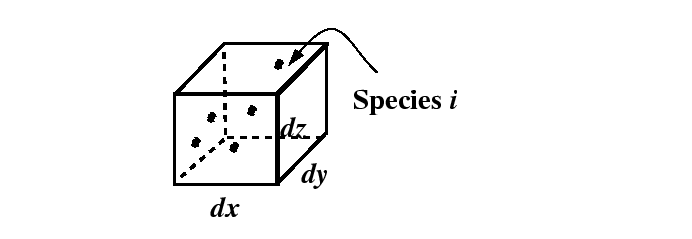 |
Figure:
Behavior of the concentration at a point
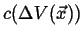 as the volume
shrinks towards the point
as the volume
shrinks towards the point 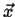 .
.
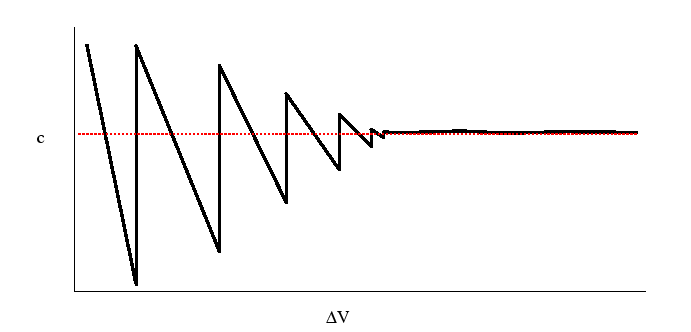 |
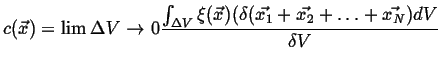 |
(01-7) |
Figure:
The function
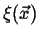 performs a weighted sampling of points near
performs a weighted sampling of points near
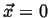 .
.
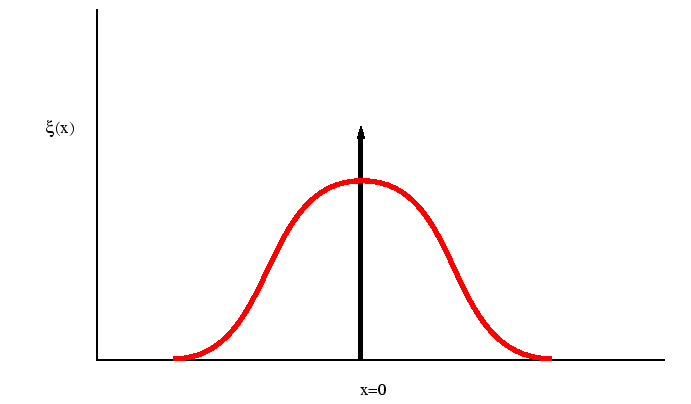 |
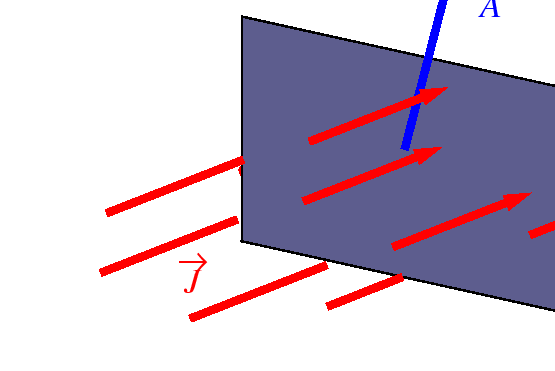
- Fluxes
- Let
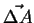 be an oriented patch of area,
be an oriented patch of area,
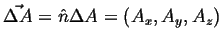 .
If
.
If 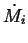 is the rate at which
is the rate at which 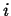 flows through
a unit area, it follows that
flows through
a unit area, it follows that
Figure:
The vector
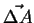 .
.
 |
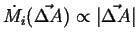 |
(01-8) |
The proportionality factor must be a vector field:
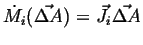 |
(01-9) |
This defines the local flux as the continuum limit of:
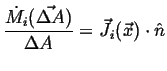 |
(01-10) |
- Accumulation
- The rate at which
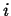 accumulates in a volume
accumulates in a volume
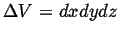 (with outward oriented normals)
during time interval
(with outward oriented normals)
during time interval 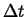 is:
is:
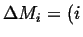 Flowing in Flowing in 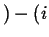 Flowing out Flowing out 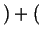 Rate of Production of Rate of Production of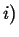 |
(01-11) |
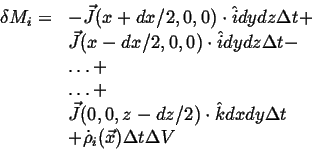 |
(01-12) |
where
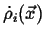 is the density of the rate of production of
is the density of the rate of production of 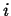 in
in 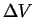 .
.
Expanding to first order in
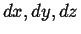 , subtracting, and using the continuum limit,
, subtracting, and using the continuum limit,
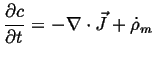 |
(01-13) |
The rate of accumulation of the density of an extensive quantity is minus the
divergence of the flux of that quantity plus the rate of production
Note that Eq. 1-13 could have been derived directly from:
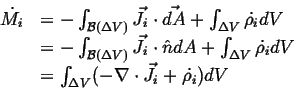 |
(01-14) |
where
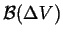 is the oriented surface around
is the oriented surface around  and the
and the



Next: About this document ...
W. Craig Carter
2002-02-06
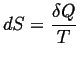
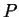 and
and 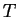 ),
then there exists a free energy function for that system (e.g.,
),
then there exists a free energy function for that system (e.g., 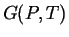 )
that is minimized at equilibrium.
Therefore, a necessary condition for equilibrium is that every small variation
in
)
that is minimized at equilibrium.
Therefore, a necessary condition for equilibrium is that every small variation
in 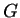 must be non-negative:1
must be non-negative:1
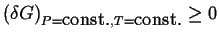 .
.