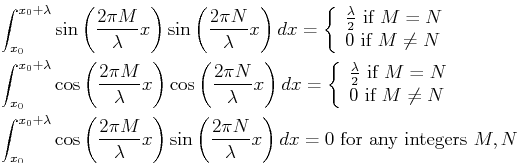 |
(27-1) |
The trigonometric functions have the property that they are orthogonal, that is:
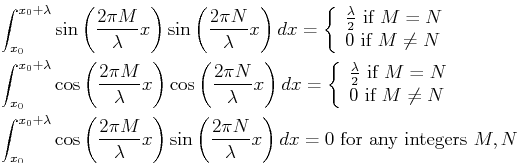 |
(27-1) |
This property allowed the Fourier series to be obtained by multiplying a function by one of the basis functions and then integrating over the domain.
For the trignometric functions, the inner product was a fairly obvious choice:
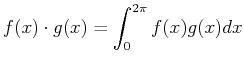 |
(27-2) |
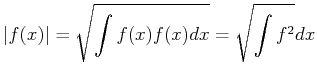 |
(27-3) |
However, there are different choices of inner products.
For example,
the Laguerre polynomials (or Laguerre functions) ![]() defined by
defined by
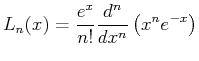 |
(27-4) |
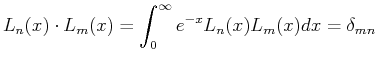 |
(27-5) |
Many ordinary differential equations--including the harmonic oscillator, Bessel, and Legendre--can be written in a general form:
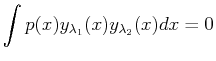 if if |
(27-7) |
The same "trick" of multiplying a function by one of the eigensolutions and then summing a series can be used to generate series solutions as a superposition of eigensolutions.
|
MATHEMATICA |
| (notebook Lecture-27) |
| (html Lecture-27) |
| (xml+mathml Lecture-27) |
| Legendre functions
|