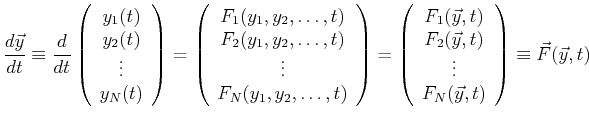 |
(25-1) |
The behavior of systems of first-order equations can be visually interpreted by plotting
the trajectories
![]() for a variety of initial conditions
for a variety of initial conditions
![]() .
An illustrative example is provided by the equation for the pendulum,
.
An illustrative example is provided by the equation for the pendulum,
![]() .
can be re-written with the angular momentum
.
can be re-written with the angular momentum ![]() as the system of first-order ODEs
as the system of first-order ODEs
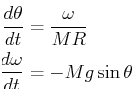 |
(25-2) |
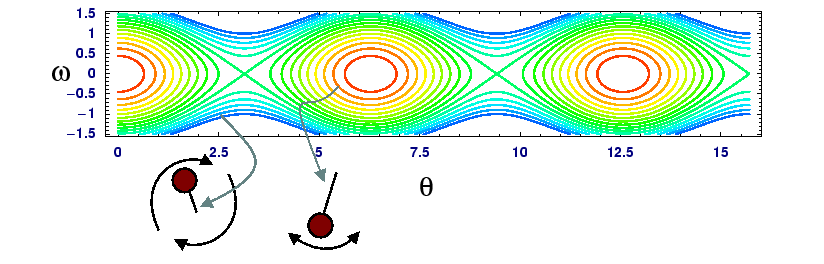
Behavior for a wide variety of initial conditions can be comprehended by the following approach:
The
![]() are the eigenvectors of Eq. 25-4
and the diagonal component is its associated eigenvalue.
are the eigenvectors of Eq. 25-4
and the diagonal component is its associated eigenvalue.
If the eigenvalue is imaginary, then the trajectory will circulate about the fixed point with a frequency proportional the eigenvalue's magnitude.
If the eigenvalue, ![]() is complex, its trajectory will both circulate with a frequency
proportional to its imaginary part and diverge from or converge to the fixed point
according to
is complex, its trajectory will both circulate with a frequency
proportional to its imaginary part and diverge from or converge to the fixed point
according to
![]() Re
Re![]() .
.
If any one of the fixed points has an eigenvalue with a positive real part, the fixed point cannot be stable--this is because ``typical'' points in the neighborhood of the fixed points will possess some component of the unstable eigenvector.