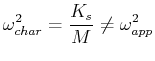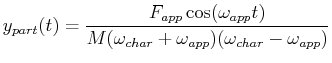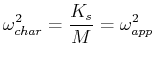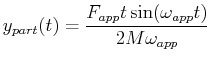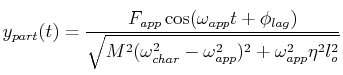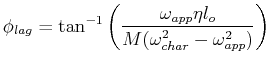Next: Index
Up: Lecture_23_web
Previous: Lecture_23_web
Next: Index
Up: Lecture_23_web
Previous: Lecture_23_web
Subsections
The physics of an isolated damped linear harmonic oscillator follows
from the behavior of the homogeneous equation:1
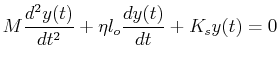 |
(23-1) |
The zero on the right-hand-side of Eq. 23-1 implies that
there are no external forces applied to the system.
The system oscillates with a characteristic frequency
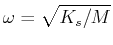 with amplitude that are damped by a characteristic time
with amplitude that are damped by a characteristic time
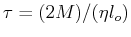 (i.e., the amplitude is damped
(i.e., the amplitude is damped
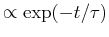 .)
.)
A general model for a damped and forced harmonic oscillator is
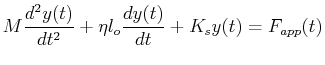 |
(23-2) |
where 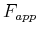 represents a time-dependent applied force to the
mass
represents a time-dependent applied force to the
mass 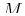 .
.
General Solutions to Non-homogeneous ODEs
Equation 23-2 is a non-homogeneous ODE--the
functions and its derivatives appear on one side and an arbitrary
function appears on the other.
The general solution to Eq. 23-2 will be the
sum of two parts:
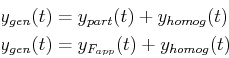 |
(23-3) |
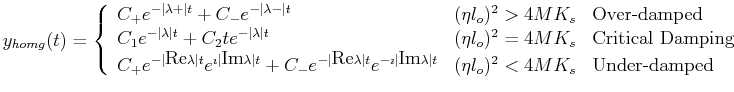 |
(23-4) |
where
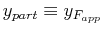 is the solution for the
particular
is the solution for the
particular 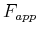 on the right-hand-side and
on the right-hand-side and  is
the solution for the right-hand-side being zero.
Adding the homogeneous solution
is
the solution for the right-hand-side being zero.
Adding the homogeneous solution  to the particular solution
to the particular solution
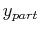 is equivalent to
adding a ``zero'' to the applied force
is equivalent to
adding a ``zero'' to the applied force 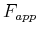
Interesting cases arise when the applied force is periodic
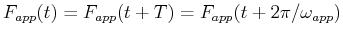 , especially
when the applied frequency,
, especially
when the applied frequency,
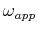 is close to the the characteristic
frequency of the oscillator
is close to the the characteristic
frequency of the oscillator
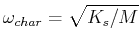 .
.
Modal Analysis
For the case of a periodic forcing function, the time-dependent force
can be represented by a Fourier Series.
Because the second-order ODE (Eq. 23-2) is linear,
the particular solutions for each term in a Fourier series can be
summed.
Therefore, particular solutions can be analyzed for one trigonometric
term at a time:
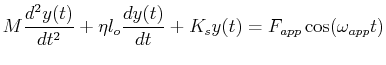 |
(23-5) |
There are three general cases for the particular solution:
| |
Condition |
Solution for
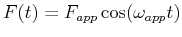
|
| Undamped,
Frequency-Mismatch |
|
|
| Undamped,
Frequency-Matched |
|
|
| Damped |
|
|
The phenomenon of resonance can be observed as the driving frequency
approaches the characteristic frequency.
Resonance can have catastrophic or amusing (or both) consequences:

Figure:
Picture and illustration of the bells at Kendall square.
Many people shake the handles vigorously
but with apparently no pleasant effect.
The concept of resonance can be used to
to operate the bells efficiently
Perturb the handle slightly
and observe the frequencies of the the pendulums--select one
and wiggle the handle at the pendulum's characteristic frequency.
The amplitude of that pendulum will increase and eventually strike
the neighboring tubular bells.
From Cambridge Arts Council Website:
http://www.ci.cambridge.ma.us/~CAC/public_art_tour/map_11_kendall.html
Artist: Paul Matisse
Title: The Kendall Band - Kepler, Pythagoras, Galileo
Date: 1987
Materials: Aluminum, teak, steel
Handles located on the platforms allow passengers to play these
mobile-like instruments, which are suspended in arches between the tracks,
"Kepler" is an aluminum ring that will hum for five minutes after
it is struck by the large teak hammer above it.
"Pythagoras" consists of a 48-foot row of
chimes made from heavy aluminum tubes
interspersed with 14 teak hammers.
"Galileo"
is a large sheet of metal that rattles thunderously
when one shakes the handle.

|

Figure:
The Tacoma bridge disaster is perhaps one of the most well-known
failures that resulted directly from resonance phenomena.
It is believed that the
the wind blowing across the bridge caused the bridge to
vibrate like a reed in a clarinet.
(Images from Promotional Video Clip from
The Camera Shop 1007 Pacific Ave.,
Tacoma, Washington Full video Available http://www.camerashoptacoma.com/)
 |
© W. Craig Carter 2003-, Massachusetts Institute of Technology
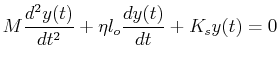
![]() with amplitude that are damped by a characteristic time
with amplitude that are damped by a characteristic time
![]() (i.e., the amplitude is damped
(i.e., the amplitude is damped
![]() .)
.)
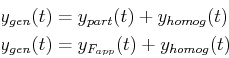
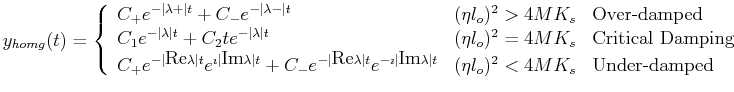
![]() , especially
when the applied frequency,
, especially
when the applied frequency,
![]() is close to the the characteristic
frequency of the oscillator
is close to the the characteristic
frequency of the oscillator
![]() .
.