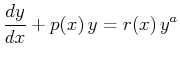Link to Current (updated) notes

Example: The Bernoulli Equation

The linear first-order ODEs always have a closed form solution in terms of integrals. In general non-linear ODEs do not have a general expression for their solution. However, there are some non-linear equations that can be reduced to a linear form; one such case is the Bernoulli equation:

$$\ensuremath{\frac{d{y}}{d{x}}} + p(x) y = r(x) y^a$$ (20-21)

Reduction relies on a clever change-of-variable, let $u(x) = [y(x)]^{1-a}$ , then Eq. 20-21 becomes

$$\ensuremath{\frac{d{u}}{d{x}}} + (1-a) p(x) u = (1-a) r(x)$$ (20-22)

which is a linear heterogeneous first-order ODE and has a closed-form solution.

MATHEMATICA$^{\text{\scriptsize {\textregistered }}}$ Example

(notebook Lecture-20)

(html Lecture-20)

(xml+mathml Lecture-20)

Converting a Nonlinear into a Linear ODE

Use MATHEMATICA$^{\text{\scriptsize {\textregistered }}}$ to show the steps that reduce Bernoulli's equation to a linear form.

Illustration of a Numerical Solution to a Non-linear First-Order ODE