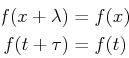 |
(17-1) |
Periodic functions should be familiar to everyone. The keeping of time, the ebb and flow of tides, the patterns and textures of our buildings, decorations, and vestments invoke repetition and periodicity that seem to be inseparable from the elements of human cognition.1
A function that is periodic in a single variable can be expressed as:
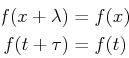 |
(17-1) |
Specification of a periodic function, ![]() , within one period
, within one period
![]() defines the function everywhere.
The most familiar periodic functions are the trigonometric functions:
defines the function everywhere.
The most familiar periodic functions are the trigonometric functions:
| (17-2) |
|
MATHEMATICA |
| (notebook Lecture-17) |
| (html Lecture-17) |
| (xml+mathml Lecture-17) |
|
Making Periodic Functions
Periodic functions are often associated with the ``modulus'' operation.
Mod |