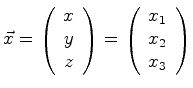 |
(07-12) |
Consider the position vector
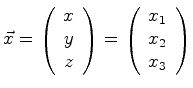 |
(07-12) |
The vectors ![]() ,
, ![]() , and
, and ![]() can be
used to generate any general position by suitable scalar
multiplication and vector addition:
can be
used to generate any general position by suitable scalar
multiplication and vector addition:
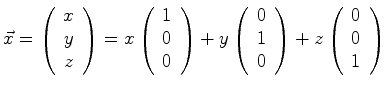 |
(07-13) |
Thus, three dimensional real space is ``spanned'' by
the three vectors: ![]() ,
, ![]() , and
, and ![]() .
These three vectors are candidates as ``basis vectors for
.
These three vectors are candidates as ``basis vectors for ![]() .''
.''
Consider the vectors ![]() ,
, ![]() , and
, and ![]() for
real
for
real ![]() .
.
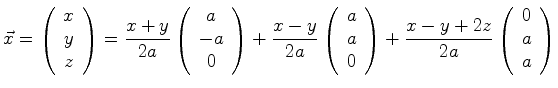 |
(07-14) |
So ![]() ,
, ![]() , and
, and ![]() for
real
for
real ![]() also are basis vectors and can be
used to span
also are basis vectors and can be
used to span ![]() .
.
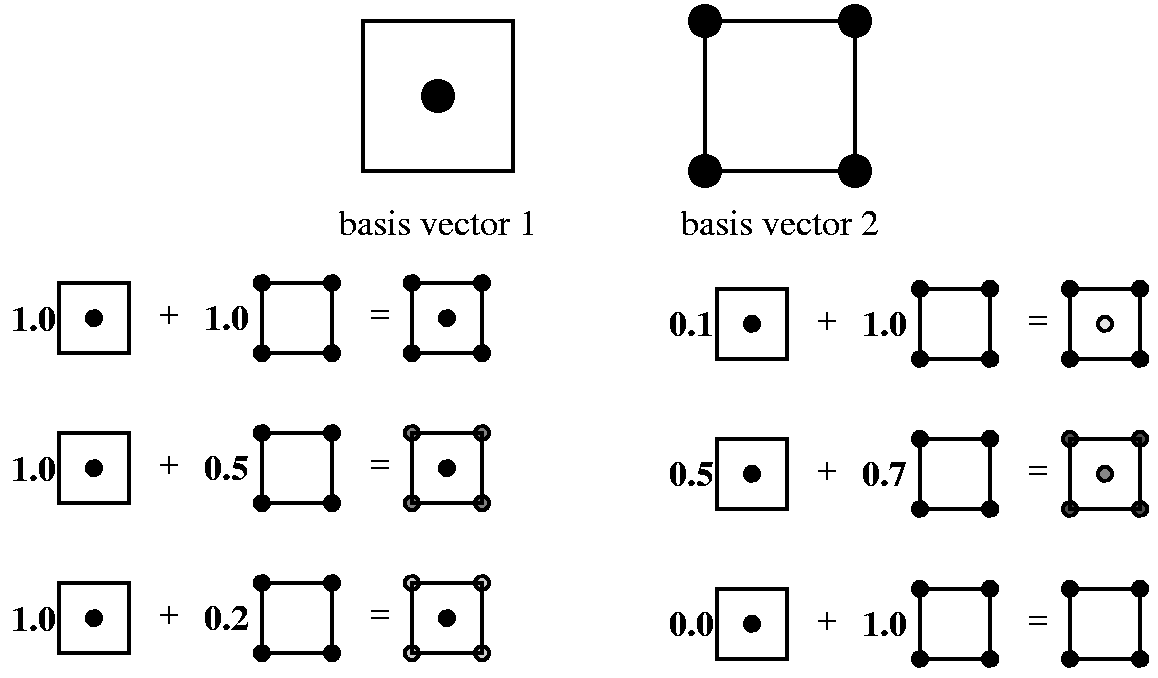
The idea of basis vectors and vector spaces comes up frequently in the mathematics of materials science. They can represent abstract concepts as well as shown by the following two dimensional basis set:
|
|