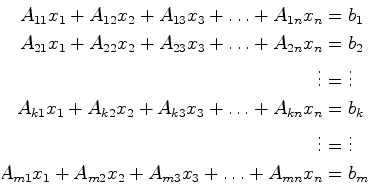Link to Current (updated) notes

Uniqueness and Existence of Linear System Solutions

It would be useful to use the Mathematica Help Browser and look through the section in the Mathematica Book: Advanced Mathematics/ Linear Algebra/Solving Linear Equations

$$\begin{split}A_{11} x_1 + A_{12} x_2 + A_{13} x_3 + \ldots + ... ...{m2} x_2 + A_{m3} x_3 + \ldots + A_{mn} x_n & = b_m \end{split}$$ (07-1)

$$A_{ij} x_i = b_j$$ (07-2)

$$\mat {A} \vec{x} = \vec{b}$$ (07-3)

MATHEMATICA$^{\text{\scriptsize {\textregistered }}}$ Example

(notebook Lecture-07)

(html Lecture-07)

(xml+mathml Lecture-07)

Properties of Determininants

$$\det \mat {A} = \det \left( \begin{array}{cccc} 1 & 2 & 1 & 1\ -1 & 4 & -2 & 0\ 1 & 2 & 4 & 5\ 1 & 0 & 1 & 1\ \end{array} \right) = 14$$ (07-4)

$$\mat {A} \vec{x} = \left( \begin{array}{c} a\ b\ c\ d \end{array} \right) \vec{x} = \left( \begin{array}{c} \frac{a + b - 2c +9d}{7}\ \fra... ...3a - 8b + 2c - 23d}{14}\ \frac{-15a + 6b + 2c + 19d}{14}\ \end{array} \right)$$ (07-5)

Taking the matrix A, and replacing the third row by a linear combination ( $p\times$first row$+ q\times$second row$+ r\times$fourth row ) of the other rows:

$$\det \mat {A_o} = \det \left( \begin{array}{cccc} 1 & 2 & 1 & 1\\... ... q + r & 2p + 4q & p -2 q + r & p + r\ 1 & 0 & 1 & 1\ \end{array} \right) = 0$$ (07-6)

$$\mat {A_o} \vec{x} = \left( \begin{array}{c} a\ b\ c\ d \end{array} \right) \vec{x}$$ (07-7)

Homogeneous Equation

$$\mat {A_o} \vec{x} = \left( \begin{array}{c} 0\ 0\ 0\ 0 \end{array} \right) \vec{x} = \left( \begin{array}{c} -2 \chi\ 0\ \chi\ \chi \end{array} \right)$$ (07-8)

Uniqueness of solutions to the nonhomogeneous system

$$\mat {A} \vec{x} = \vec{b}$$ (07-9)

Uniqueness of solutions to the homogeneous system

$$\mat {A} \vec{x_o} = \vec{0}$$ (07-10)

Adding solutions from the nonhomogeneous and homogenous systems

You can add any solution to the homogeneous equation (if they exist there are infinitely many of them) to any solution to the nonhomogeneous equation and the result is still a solution to the nonhomogeneous equation.

$$\mat {A} (\vec{x} + \vec{x_o}) = \vec{b}$$ (07-11)