Nucleation and Growth

Nucleation of a new phase occurs when a phase in an alloy of composition $\ensuremath{{X}_\circ}$ is unstable with respect a composition that is not near $\ensuremath{{X}_\circ}$.

Figure 32-13: Example of a phase diagram that might require nucleation and growth for a phase transformation to occur. Suppose that an $\beta$-phase at composition $\ensuremath {{X}_\circ }$ is quickly cooled into the two-phase ($\alpha$-$\beta$) region and then the transformation to the equilibrium phases and compositions is allowed to occur.

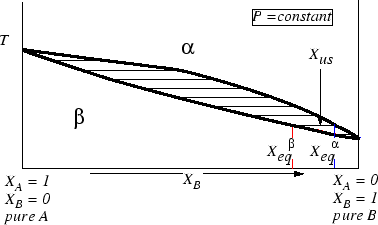The transformation will require nucleation of an $\alpha$-phase at a composition that, when combined with the molar free energy of the resultant $\alpha$-phase, gives a mixture with a molar Gibbs free energy that is less than the value of $\ensuremath{\overline{G^\beta}}(\ensuremath{{X}_\circ})$

In other words, $\partial^2 \ensuremath{\overline{G}}/\partial X^2 > 0$ at $X=\ensuremath{{X}_\circ}$, but there is some $X^{\mbox{nuc}}$ for which $\ensuremath{\overline{G^{\mbox{mixture}}}}(\ensuremath{\lan... ...suremath{{X}_\circ}) = \Delta \ensuremath{\overline{G}}^{\mbox{nuc}} < 0$. The negative $\Delta \ensuremath{\overline{G}}^{\mbox{nuc}}$ is the driving force for the creation of a new phase.

Figure 32-14: Illustration of the driving force for nucleation derived from the molar Gibbs free energies of solution for the case where the nucleated $\alpha$-phase appears at its equilibrium composition $X^\alpha _{eq}$ at the expense of enriching the $B$-composition of the $\beta$-phase to its equilibrium concentration $X^\beta _{eq}$. $\Delta \ensuremath{\overline{G^{\mbox{nuc}}}}$ is the (negative) distance between the $\beta$-phase solution free energy curve and the common tangent. $\Delta \mu _A$ is the difference of the two tangents, evaluated at the pure $A$ axis. Similarly, $\Delta \mu _B$ is the difference extrapolated to the pure $B$ axis. 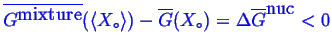Because $\Delta \mu_A = \mu_A^\alpha - \mu_A^{\mbox{unstable}}(\ensuremath{{X}_\circ})$ is negative, there is a driving force for the $A$-component to diffuse towards a nucleating $\alpha$ phase from the parent unstable phase.

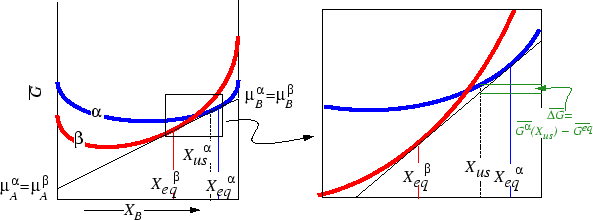Notice that the driving force for the phase transformation goes away as the unstable composition $\ensuremath{{X}_\circ}$ approaches the limiting compositions on the tie-line.

The driving force for nucleation is important because it has to be utilized to overcome the additional energy associated with the interface between the $\alpha$ and the $\beta$ phase. This is the interfacial energy.

The surface (or interfacial) tension is the amount of energy that is required to produce interface per unit area interface. Let the interfacial tension between the $\alpha$ and the $\beta$ phase be $\gamma^{\alpha \beta}$ and suppose that when the $\alpha$-phase nucleates, that it forms a little sphere of radius $R$:

Figure 32-15: Illustration of the nucleation process.

The total (extensive) extra energy required for the phase transformation is:

$$\input{equations/nucleation-surface}$$ (32-18)

Therefore the total free energy required to create a nucleus is given by

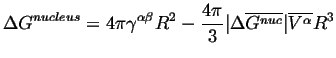$$\input{equations/nucleation-total}$$ (32-19)

where $\vert\Delta \ensuremath{\overline{G^{nuc}}}\vert$ is the (magnitude) of the molar driving force to create the nucleating $\alpha$-phase and $\ensuremath{\overline{V^\alpha}}$ is its molar volume.

Therefore the total energy has contributions from two parts:

Figure 32-16: Total (spherical) nucleation energy as a function of nucleus size. The interfacial contribution opposes nucleation while the volumetric driving force propels nucleation. A small sizes, the interfacial term dominates and nucleation is prevented. At larger sizes, the volumetric term dominates.

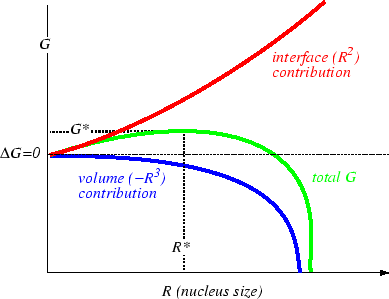If a nucleus can attain a size that exceeds the maximum, $G^*$ of the curve in Fig. 32-16, then it can increase its size while continuously decreasing its free energy--therefore any nucleus with size $R^*$ or larger will grow continously.

To calculate this critical size, take the derivative of Eq. 32-19 and set it equal to zero and solve for $R$:

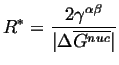$$\input{equations/nucleation-size}$$ (32-20)

and substituting this radius into the expression for the nucleation energy gives the nucleation barrier energy:

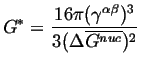$$\input{equations/nucleation-energy}$$ (32-21)

This expression illustrates that nucleation must occur at a critical size and that the energy barrier to nucleation can be reduced by a decrease in the interfacial tension or by an increase in the volumetric driving force.³The time required for the phase transition to occur is related to the time required for a critical composition fluctuation to occur that will produce a critical nucleus of size $R^*$--and that time increases exponentially with the barrier $G^*$.