Behavior of the Regular Solution Model

Above, a ``first-order'' correction to the ideal solution model based on an atomic averaging for the enthalpy of mixing.

This is called the regular solution model.

$$\input{equations/24-1A}$$ (32-10)

where

$$\input{equations/24-1B}$$ (32-11)

and

$$\input{equations/24-1C}$$ (32-12)

Consider both terms:

Figure 32-1: The behavior of enthalpy in the regular solution model.

Note that $\omega < 0$ favors mixing, and makes sense because $\omega_{AB}$ is more negative than $\ensuremath{\langle \omega_{AA} + \omega_{BB} \rangle}$.

Figure: The behavior of the ideal entropy of mixing: $\Delta \ensuremath{{\ensuremath{\overline{S}}}^{\mathcal{IS}}} = -R(X_A \log X_A + X_B \log X_B)$

So that, taken together: $\Delta \ensuremath{\overline{G^{mix}}} = \Delta \ensuremath{\overline{H^{mix}}} - T \Delta \ensuremath{\overline{S^{mix}}}$:

Figure 32-3: The behavior of the molar Gibbs free energy of mixing for the regular solution.

Note that the limiting behavior for pure or extremely dilute solutions is dictated by:

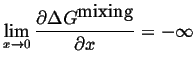$$\input{equations/24-3A}$$ (32-13)

A solution can always lower its free energy by dissolving at least a small amount component. There is thermodynamically always some finite solubility (but it can be, and often is, very, very small). This implies that the width of a single-phase region must always be finite.

Consider the case where $\omega > 0$, so the system will tend to ``unmix'' at low temperatures.

Figure 32-4: The dependence of the regular solution model on temperature for $\omega > 0$. At low temperatures, the curve develops a ``self-common-tangent'' and is thus unstable at compositions within the tangent points with respect a decomposition into a composition-rich and a composition-poor phase.

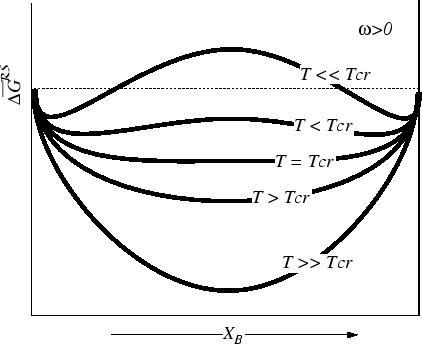For the case of a regular solution, the curve is symmetric around $X = 1/2$, and in this case we can calculate the positions of the common tangents:²

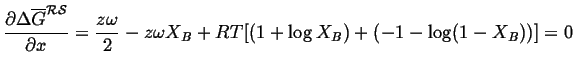$$\input{equations/24-4A}$$ (32-14)

However, this is hard to solve (see Equation 32-15).

The critical temperate can be determined analytically by noting that as the common tangents form that the curvature changes sign at $X_B = 1/2$.

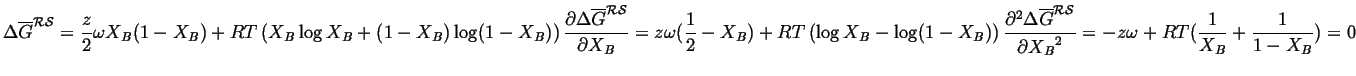$$\input{equations/24-5A}$$ (32-15)

At $X_B = 1/2$, the zero first appears at

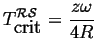$$\input{equations/Tcr}$$ (32-16)