Non-Ideal Solution Behavior

In this section, a simple model for the enthalpy of mixing will be derived. It will be shown that a positive enthalpy of mixing tends to make a system separate and have a miscibility gap at low temperature. A negative enthalpy of mixing tends to favor stable homogeneous solutions.

Consider two neighbors in a solution. The probability that one of the neighbors is an $A$-type or a $B$-type is simply:

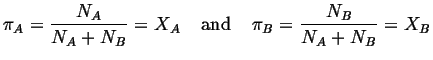$$\input{equations/probs}$$ (32-1)

Therefore the probability that a given ``bond'' is an $A$- $B$ type is:

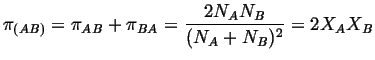$$\input{equations/23-5A}$$ (32-2)

If each atom has $z$ nearest neighbors, the number of bonds, total, is

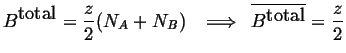$$\input{equations/23-5B}$$ (32-3)

The bond density of $A$- $B$ type is therefore:

$$\input{equations/23-6A}$$ (32-4)

If the energy per $A-B$ bond is $\omega_{AB}$¹then the enthalpy density (due to the $A$- $B$ bonds) is:

$$\input{equations/23-6B}$$ (32-5)

Similarly, the bond density of $A$-types is $\ensuremath{\overline{B}}_{AA} = \frac{z}{2} X_A X_A$ so that $\ensuremath{\overline{H_{AA}}} = \frac{z}{2}X^2_A \omega _{AA}$. Similarly $\ensuremath{\overline{H_{BB}}} = \frac{z}{2}X^2_B \omega_{BB}$.

Putting this all together

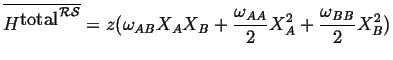$$\input{equations/23-6C}$$ (32-6)

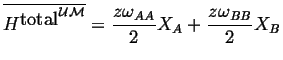$$\input{equations/23-6D}$$ (32-7)

Therefore since, ${\Delta \ensuremath{\overline{H_{mixing}}}} = \ensuremath{\overline{H^{sol}}} - \ensuremath{\overline{H^{pure\;mix}}}$:

$$\input{equations/23-7A}$$ (32-8)

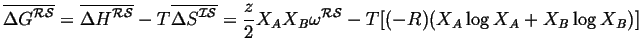$$\input{equations/G-mix-RS}$$ (32-9)

This is the Regular Solution Model