Next: Alternative Statements of the Up: Lecture_13_web Previous: The Second Law of

An Illustrative Example

Consider the passage of heat from a hot body to a cold one, with no other work being performed.

Consider two very large bodies, one at $\bgroup\color{blue}$ T=400$\egroup$ K and the other at $\bgroup\color{blue}$ T=300$\egroup$ K (The bodies are so BIG that there temperatures are roughly constant for the passage of a small amount of heat between them.)

**Figure 13-1:** A common process, one that you might see every day.
$\begin{figure}\resizebox{6in}{!} {\epsfig{file=figures/8-5.eps}} \end{figure}$

Case 1

Suppose 400 joules of heat are transferred from the hot object to the cooler object .

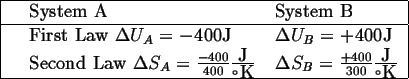
$\begin{center}\vbox{\input{tables/tab85} }\end{center}$

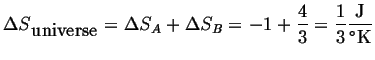$\displaystyle \input{equations/85A}$

(13-1)

Case 2

Suppose that, somehow, the same amount of heat (400 J) is transferred from the cooler to the hotter body.

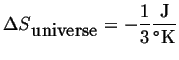$\displaystyle \input{equations/86A}$

(13-2)

This is not observed.

Suppose that the bodies in Figure 13-1 are not so BIG this time and that they have a finite heat capacity, but suppose that the thermal conductivity of each body alone is very large compared to the thermal conductivity of the ``stuff that allows heat to transfer between them.'' In other words, while heat flows between the bodies, we can consider the temperature of the bodies to be uniform at all times.

Using the definition of entropy and the heat capacities of each body, how should the entropy change of the universe be calculated?

Next: Alternative Statements of the Up: Lecture_13_web Previous: The Second Law of

W. Craig Carter 2002-10-03