Gaseous Capacities at Constant Volume or Pressure

$C_V$ is the heat capacity for an ideal fluid substance for processes in which no work is done. There would be equivalent ``no-work'' heat capacity in more complex materials.

$C_P$ is the heat capacity for an ideal fluid substance for processes in which an intensive variable is held fixed.

Consider identical ideal fluid systems, that receive the exact same amount of heat by a constant volume (isochoric) process and by a constant pressure (isobaric) process:

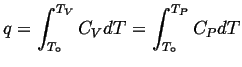$$\input{equations/two-heat-capacities}$$ (10-1)

We can make a hand-waving argument that the temperature, $T_P$, reached during the constant pressure process is smaller than $T_V$.

No work is done for the constant volume process, so $\Delta U_V = q$. Let's imagine that a new process is added to the end of the constant volume process that takes it to the same state as the end of the constant pressure process (i.e, let it expand by reducing the applied pressure). It is clear that we can extract work from this added process because the fluid can do work on its surroundings as it expands--therefore it should be possible to store this work and then pass it back to the system as heat at constant volume, thus increasing the temperature. Since the final state is the same, it follows that $T_P < T_V$, therefore, using the intermediate value theorem of basic calculus:

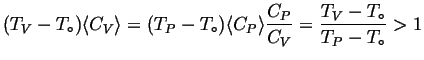$$\input{equations/cpgreater}$$ (10-2)

For larger thermal expansion, the difference in heat capacities will be greater.

Gases, which expand considerably with temperature, have a large difference in their heat capacities.

Liquids do not expand as much. For H$_2$O at ${15}^\circ$C and $P=1$ atm, $c_P = 1$   cal$/({}^\circ$   K   gram$)$. (Note use of little $c$ for the derived intensive quantity on a per mass basis), and $c_V$ is only slightly different.

For solids, the difference is very small and usually neglected.