Some Example State Functions

Pressure could be a state function of the variables, $N$ the number of atoms present, $V$ the volume of the container, and $T$ the temperature:

$$\input{equations/eq-state-1}$$ (04-1)

This says that we can pick any of the three and the fourth is determined by equilibrium properties of the material.

Note that the word pressure plays two roles here! One role is as a thermodynamic variable that could be measured and the other is the name of some function. Another way to think of this is that for an arbitrary system, there is no reason to expect that there might be a function called pressure that relates to only $N$, $V$, and $T$ but there is nothing preventing us from measuring the pressure anyways. However, if we are considering an ideal gas model for our system, then there is a function $P = P(N,V,T)$ which tells us that we need not bother to measure $P$ if we know $N$, $V$, and $T$--or we can use our knowledge of $P(N,V,T)$ for an ideal gas to construct a pressure gauge.

Another state function is total number of molecules or atoms:

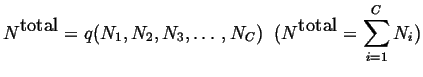$$\input{equations/eq-state-3}$$ (04-2)

Total mass:

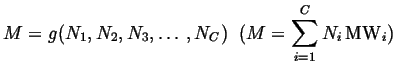$$\input{equations/eq-state-2}$$ (04-3)