Summary

The three calculations using Evolver which have been demonstrated are fairly disparate examples of useful computations in materials science. There are many more which will be described in a future publication. The purpose in this paper was to introduce Evolver to members of the materials science community as new research tool-hopefully with enough working (and hopefully motivating) examples that new challenging materials science problems can be tackled with Evolver .

Ken Brakke, the mathematician who wrote Evolver, deserves an enormous amount of credit. Since materials science tends to be such an eclectic discipline, it is very useful to absorb progress from different disciplines. There is a richness of mathematical ideas in Evolver, after all it was written with problems in mathematics in mind. Nevertheless, materials scientists will use new tools where they can find them.

One reason that Evolver is so useful is that it is a programming language. This gives it useful features; Evolver is:

Flexible

It can be used to solve an enormous range of problems. The concept of an Evolver mesh need not even be geometric, but any data structure that can mapped onto an Evolver mesh could be minimized. Because parameters need not be fixed, but can be changed on the fly, the code is re-usable.

Progammable

One can query variables, calculate expressions and then have Evolver act in a controlled fashion according to the result. New macros and functions can be written in-situ. There are very many ways to add energies to elements; the Evolver manual describes about 40 and more are always being added.

Quantitative

It is possible to get real numbers out of Evolver such as those which were used to make the plots in Figure 3. One can also obtain quite general information, for instance in one application it was important to find how a contact angle was changing on a constraint. The following Evolver command was able to extract the information: foreach edge ee where on_constraint 1 do { foreach ee.vertex do
{printf "%g %g %g 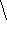n",x,y,z}; foreach ee.facet fff do
{ foreach fff.vertex do {printf "%g %g %g 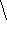n",x,y,z}\} }. This printed the positions of the ends of each edge on a constraint, and then printed the positions of the corners of the facet belonging to that edge. In turn, this later served as input to some auxiliary code which calculated the contact angle as a function of position.

Visual

Seeing the result is very important and certainly one of the best ways to learn more about the problem being solved.

Extensible

Instructions for adding source code to Evolver is included with the distribution. Invariably, one wants to try something new and since the source is free it's possible to try anything. A good example is an Evolver calculation on line energies referred to in these proceedings by Jennifer Kelley.

The bottom line is that one doesn't have to write a minimization algorithm. It becomes necessary only to concentrate on the problem at hand. However, there is still some work involved. An initial mesh needs to be constructed. There is some art in maintaining a good mesh by judiciously deleting and refining elements. And there is some cleverness required in the application of the Stoke's and the divergence theorems.

One of the most useful ways to get started is to adapt some working Evolver code; such working codes, including the ones described in this paper are available on the net[5].