Next: About this document
Up: No Title
Previous: References
Figure 1: In the left column molar free energies for
the regular solution
model at temperatures 
, 
, 
are
plotted. The chemical potentials at corresponding temperatures are
plotted on the right; these curves trace out the "
-shapes."
The phase diagram is plotted for reference in the center.
The crossings in the -shapes represent of two-phase equilibria. The
compositions 
are given by the normals to curve and
the two compositions in equilibrium at the crossing are also the
common tangent points which could be drawn on 
. The ears represent
metastable and unstable compositions; the sharp points on the ears are the
spinodal points which are
represented by dashed lines on the phase diagram, or points
of inflection on .
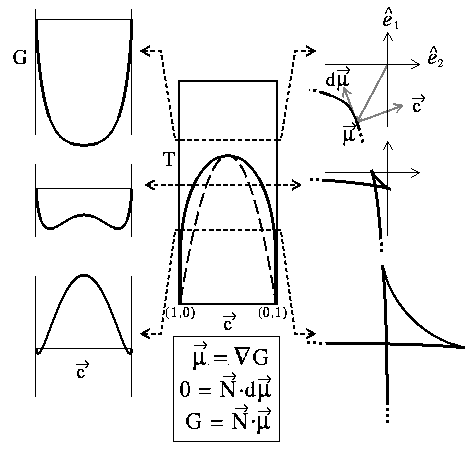
Figure 2: An analogous construction to that
in Fig. 1 for an anisotropic 
for various values of an
anisotropy parameter 
(see text).
In the left column is plotted from top to bottom for
, 1, 2.
Anisotropy increases with positive , so 
is
used in the 
-diagram to correspond to the temperature
axis in Fig. 1.
The shape resulting from the gradient construction-with the
ears removed-is the surface of the Wulff shape.
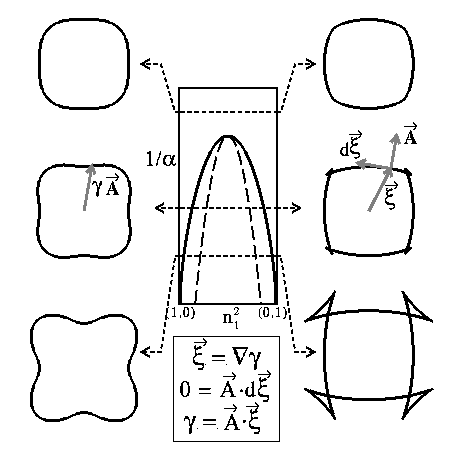
Figure 3:/b> Illustration
of the chemical Wulff construction.
In the left figure, the molar free energy is plotted for a regular solution at
. In the middle two figures the Euclimolar free energy
(see text) for the same temperature
is graphed as heavy curves in standard format and radially as 
. Note that the second and third plots look convex.
In the third panel, one step in the chemical Wulff construction is illustrated.
At a particular composition on 
a half plane is constructed
which is normal to radius (thin black line) drawn from the origin.
This divides the composition space into two parts: the gray region is to be
discarded.
In the final panel, the iterative elimination of discarded space yields the
chemical Wulff shape.
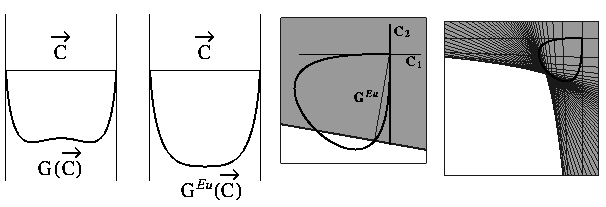
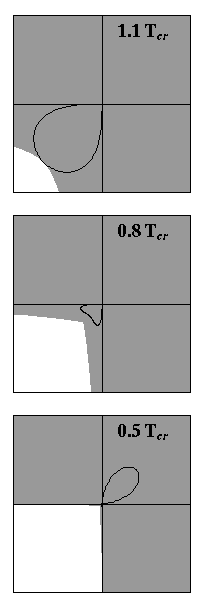
Figure 4: Illustration
of the chemical Wulff construction for the three temperatures
which were used in 1.
The borders of the Wulff shapes are the same
as the -shapes without ears.
Next: About this document
Up: No Title
Previous: References