 |
Last time
Morphological Stability of a Growing Spherical Precipitate
Kinetics of Nucleation and Growth Transformations -- No Composition Change
Time Cone; Poisson Probability Distribution
Nucleation, Growth, Transformations, Coarsening,
and Grain Growth: Reprise
It is useful to review how all of the kinetic processes associated with microstructural evolution relate to one another. We have been discussing how a transformation proceeds when a system is out of equilibrium, and how the kinetic processes affect the resulting microstructure.
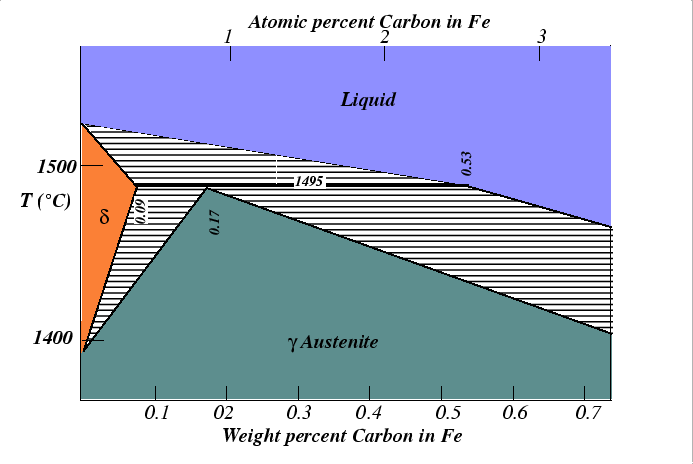
An indication of which phase transformations may occur comes from the equilibrium phase diagram, for example:
Types of Transformations The kinetics of alloy phase transformations can be categorized into two fundamental categories.
Both kinds of transformations can be illustrated in the following figure which is taken from the iron-rich end of the Fe-C phase diagram.
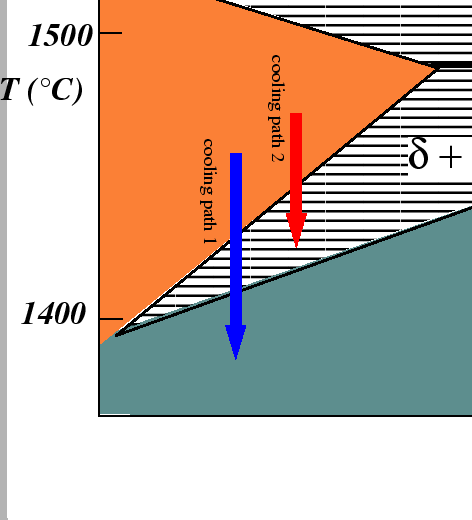 |
The two arrows represent quenching processes. The process on the left
(iron-rich) side represents
a quench from the single ![]() -phase into the single
-phase into the single ![]() -phase region.
The second
cooling path represents a quench from the
single
-phase region.
The second
cooling path represents a quench from the
single ![]() -phase into the two phase
-phase into the two phase
![]() region.
region.
It is important to realize that the cooling paths in the above equilibrium phase diagram are not sufficient for predicting what kinds of microstructures or even which phases will exist at the end of an experimental quench. If either the nucleation or the growth kinetics are slow--the usual case in solid-solid transformations--then the equilibrium phases that are predicted by the equilibrium phase diagram may not even appear. Furthermore, there may non-equilibrium phases that do not appear on the phase diagram and have lower molar free energy from than a currently existing phase. If the the non-equilibrium phase has faster nucleation kinetics, then it may appear during the quenching experiment. The essential information which does not appear in the cooling paths is the rate of quench.
Such cooling curves are illustrated in the following figure in plots of temperature versus time.
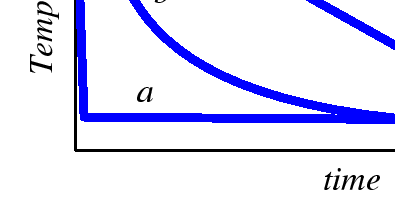 |
The three curves are each possible representations for one of the arrows illustrated on the equilibrium phase diagram. They differ in the rates of cooling. The curve a represents a very rapid quench, followed by an anneal at the final temperature. The curve c represents a constant cooling rate to the final temperature.
Consider the rapid quench illustrated by curve a. If the nucleation of
the ![]() -phase is so slow that it cannot occur during the short time
that the system spends at temperatures where the
-phase is so slow that it cannot occur during the short time
that the system spends at temperatures where the ![]() -phase is in
equilibrium
with
-phase is in
equilibrium
with ![]() , then
, then ![]() can transform to
can transform to ![]() with no change in
composition at the lower, annealing, temperature.
This is an example of a structural transformation which does not
require long-range
diffusion.
with no change in
composition at the lower, annealing, temperature.
This is an example of a structural transformation which does not
require long-range
diffusion.
For an example of a phase transformation that requires long-range
diffusion, consider
the second quench experiment illustrated in the equilibrium phase diagram.
If the same type of rapid quench is followed by a long anneal, then the new
equilibrium ![]() -phase forms at a different composition which is
given by the tie-lines in the phase diagram. In this case, carbon must diffuse
out of the parent
-phase forms at a different composition which is
given by the tie-lines in the phase diagram. In this case, carbon must diffuse
out of the parent ![]() -phase and into the growing
-phase and into the growing ![]() -phase.
Of course, the limiting fraction of the
-phase.
Of course, the limiting fraction of the ![]() -phase which can form is
given by the lever rule in the phase diagram.
-phase which can form is
given by the lever rule in the phase diagram.
For both types of transformation, nucleation (or decomposition) of the new phase is required before growth can occur. The relationship between cooling curves, phase diagrams, and transformation kinetics are understood in terms of nucleation and growth kinetics.
Nucleation
Nucleation is a competition between capillary forces that resist the creation of new interfaces and a driving force to grow a more stable phase.
The rate of nucleation depends most strongly on two energetic factors:
The equilibrium number of critical size nuclei is given by:
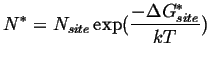 |
(35-1) |
The overall rate of nucleation, ![]() ,
is a product of the number of critical equilibrium
nuclei and the frequency that atoms successfully transfer from the parent
phase into the nucleus.
,
is a product of the number of critical equilibrium
nuclei and the frequency that atoms successfully transfer from the parent
phase into the nucleus.
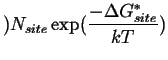 |
(35-2) |
Since the the activation energy
![]() is a linear combination
of a barrier (i.e., surface energy
is a linear combination
of a barrier (i.e., surface energy ![]() )
term plus a temperature dependent volumetric driving
force (
)
term plus a temperature dependent volumetric driving
force (
![]() ) which depends on the undercooling, the activation
energy is function of undercooling.
) which depends on the undercooling, the activation
energy is function of undercooling.
The transfer or migration activation energy is not a strong function of temperature. Therefore, according to equation 35-3, there is a maximum in the nucleation rate at finite undercoolings as illustrated in the figure below:
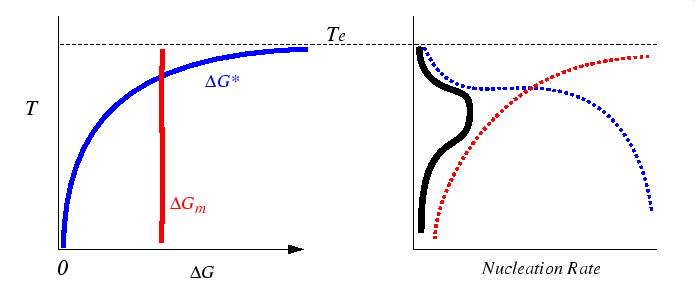 |
Growth Once an incipient nucleus has reached its critical size, the capillary forces that restricted the development of the new phase become insignificant and the kinetics for growth are dominated by the limiting kinetic mechanism and the thermodynamic driving forces.
If the transformation is of the type that requires no long-range diffusion, then the rate of growth is controlled by the rate of atomic transfer across the growing phase interface.
However, if long-range diffusion is required, then two different rate-limiting processes can affect growth rate. Each of these are temperature dependent--typically the growth rate is Arrhenius type with growth becoming very slow at low temperatures.
This case applies when the time scale for diffusivity ![]() (where
(where ![]() is the
distance over which mass is transported to the growing particles) is
small compared to thecharacteristic
time to transfer
across the interface,
is the
distance over which mass is transported to the growing particles) is
small compared to thecharacteristic
time to transfer
across the interface,
![]() .
.
In this case, the growth rate is limited by the diffusivity. As discussed previously in this course. diffusivity also has an Arrhenius relationship:
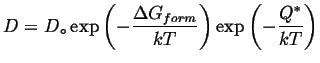 |
(35-4) |
In general, the rate of diffusional transport falls off very quickly with temperature.
Coarsening
Consider a rapid quench for `cooling path 2' in Fig. 35-2.
At short times, the microstructural development is that of nucleation and
growth of the ![]() -phase and the depletion of carbon from the
-phase and the depletion of carbon from the
![]() -phase..
However, according to the phase diagram, all of the driving force for growth
will be extinguished when a phase fraction of about 1/2 of the
-phase..
However, according to the phase diagram, all of the driving force for growth
will be extinguished when a phase fraction of about 1/2 of the ![]() -phase
is created.
-phase
is created.
Once the driving force for growth approaches zero, then the only remaining driving forces for microstructural evolution are the capillary driving forces. The capillary driving forces result in coarsening.
Note that the multiple phase region of an equilibrium phase diagram does not imply anything about how finely the phases are spatially configured--only the relative fractions and their compositions. The surface energy, through capillary driving forces, drives coarsening.
Note that the same limiting processes that were discussed for growth can also be applied to coarsening--however, with diminished driving forces. In both cases, a mean-field theory can be formulated for the rate of growth of an average particle.
Grain Growth
Consider a quench for `cooling path 1' in Fig. 35-2.
Each bit of nucleated ![]() -phase will grow until the entire
volume is transformed to
-phase will grow until the entire
volume is transformed to
![]() --in other words, growth proceeds until impingement.
If each
--in other words, growth proceeds until impingement.
If each ![]() -nucleus has a differing crystallographic orientation,
then where impingement occurs, a grain boundary will result.
-nucleus has a differing crystallographic orientation,
then where impingement occurs, a grain boundary will result.
The grain boundaries also represent extra surface energy and a different type of coarsening can occur to reduce the extra surface energy. The process of grain growth is driven by capillary forces associated with grain boundary energy.
In two dimensions, for isotropic grain boundary energy, geometric considerations alone showed that grains with more sides than six would grow at the expense of grains with fewer sides.
By contrast, coarsening of isolated particles is driving by a size effect and grain growth is driven by a geometric effect.
TTT Diagrams
Practical application of nucleation and growth kinetics is often made from Time-Temperature-Transformation (TTT) diagrams. TTT diagrams contain several curves, each representing a particular constant value fraction of total transformed volume after a particular time for a fixed annealing temperature. The diagrams are usually determined by experiment, but their common ``C''-shape follows from nucleation and growth kinetics.
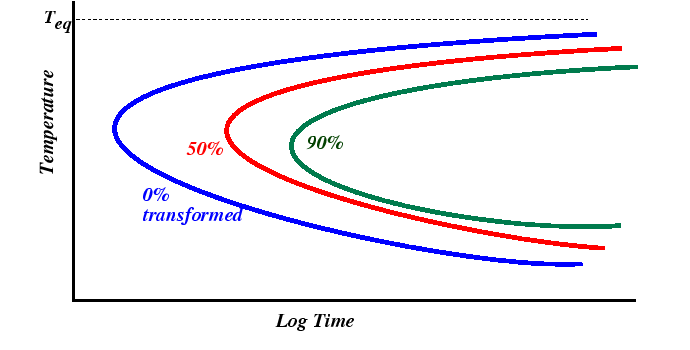 |
At temperatures just below the equilibrium transformation temperature, transformations take a long time since the nucleation rate is low. (Remember that at low driving forces, that heterogeneous nucleation is expected to dominate.) At large undercoolings, transformation times are limited by transport or by motion of atoms across the transformaion interface.
The displacement of the curves of different volume fraction follow from both JMA kinetics (discussed in the next section) and from lever-rule considerations from the equilibrium phase diagram.
Among the questions that the TTT diagram can help answer are: