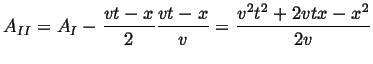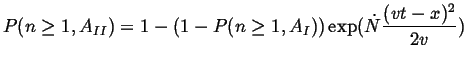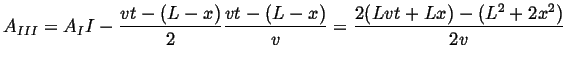Last time
Growth with moving interfaces--Stefan conditions
Solidification of Pure Substances
Diffusional Growth during Precipitation
Solidification with and without Undercooling
Shape Stability of moving interfaces; constitutional undercooling
Johnson-Mehl-Avrami: Evolution of Transformation Fraction
Consider the growth stage for the case where a parent phase will undergo a compete transformation to a new equilibrium phase. The amount of new equilibrium phase will depend on time, growth rate and the number of nuclei.
For simplicity, suppose that all the nuclei grow as spheres with constant
velocity, ![]() , and are nucleated
at some different time
, and are nucleated
at some different time ![]() .
.
The nucleus which nucleated at some time ![]() will have a volume at
time
will have a volume at
time ![]() :
:
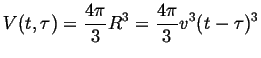 |
(34-1) |
If the nuclei do not interfere (collide during growth), then the total
volume of transformed material is the sum of all the nuclei which have
created at times ![]()
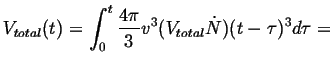 |
(34-2) |
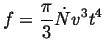 |
(34-3) |
If the nuclei do interfere with each other (a condition which would apply at either high density of nucleation sites or long times), then the above equation must be modified to account for volumes of particles which are multiply counted. If the particles are nucleated independently, then the volume fraction is given by the Avrami equation:
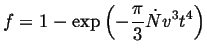 |
(34-4) |
In general, depending on whether all the nuclei appear at one time, or the dimensionality of growth, the general equation for volume transformed looks like:
| (34-5) |
Cahn's Time-Cone Analysis of JMA Kinetics The method is first described for the one-dimension case: nucleation and growth on a wire. Extensions to higher dimensional nucleation domains is straightforward.
The first step is to add a time axis to the nucleation domain as follows:
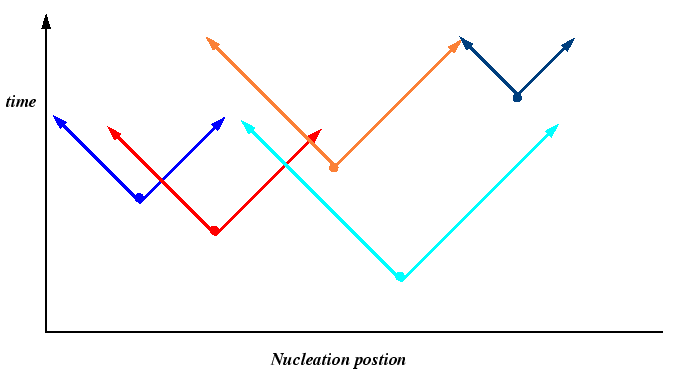 |
The small circles in the figure represent random nucleation positions and times. The lines which emanate from the nucleation positions indicate the growth fronts for the particles as a function of time as if the particles do not interact--these are called growth time-cones. If the growth rates are constant, the growth cones are truly circular conical shapes. At later times, some regions are covered by one or more growth cones. Since a particlar region cannot transform twice, it is incorrect to count the overlapping area more than once.
The actual fraction of transformed material can be determined by
turning the problem upside-down. Consider an arbitrary test point
at some time ![]() , that point will not
have been transformed if and only there is no nucleation event which
can influence that point.
The nucleation events which can influence that point lie within
a cone of influence which extends backwards in time from
that point:
, that point will not
have been transformed if and only there is no nucleation event which
can influence that point.
The nucleation events which can influence that point lie within
a cone of influence which extends backwards in time from
that point:
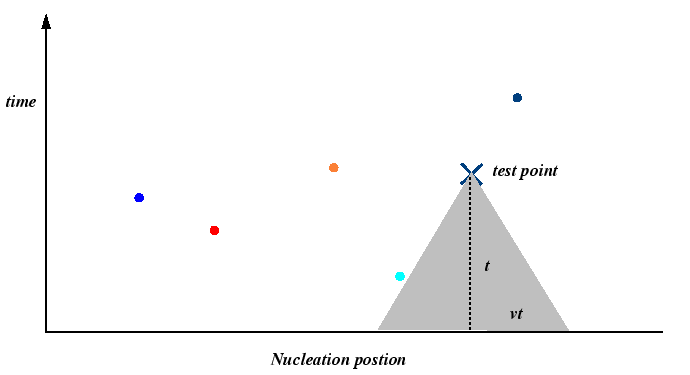 |
It is reasonable to assume that the nucleation events are random in
time--in this case, Poisson statistics apply.
In Poisson statistics, the probability of exactly ![]() events occurring
in a volume
events occurring
in a volume ![]() is given by:
is given by:
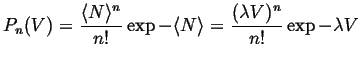 |
(34-6) |
In particular, the probability that no event occurs is
![]() ; so the probability that at least one event occurs is
; so the probability that at least one event occurs is
![]() .
For the case illustrated in the figure above, one needs to calculate
the fraction of points which are influenced by at least one event:
.
For the case illustrated in the figure above, one needs to calculate
the fraction of points which are influenced by at least one event:
| (34-7) |
For larger dimensionality nucleation domains, the calculation is quite similar:
 |
The final frame shows the cones from below (looking in direction of increasing time). Since the growth velocity is constant, the resulting microstructure after full impingement is a Voronoi tessellation.
Example of Time-Cone: Edge Effects
Consider transformation kinetics in one dimension, such as recrystallization
in a narrow wire.
For a finite wire of length ![]() , you might expect that probability that a
region will have transformed will depend on the proximity to the end of
the wire.
Investigate the end effects on transformation kinetics on a finite
length of wire
, you might expect that probability that a
region will have transformed will depend on the proximity to the end of
the wire.
Investigate the end effects on transformation kinetics on a finite
length of wire ![]() , with constant transformation growth rate
, with constant transformation growth rate ![]() (length/time) and a constant, uniform, nucleation rate
(length/time) and a constant, uniform, nucleation rate ![]() (number/(length time)).
Calculate the probability that a point
(number/(length time)).
Calculate the probability that a point ![]() will have transformed at time
will have transformed at time ![]() .
.
This problem is ideally suited for the `time-cone' method: for each point on
the wire, there an `area' in `length-time' in which if any nucleation
occurs, then ![]() will have transformed.
will have transformed.
If the nucleation events are independent, then Poisson statistics apply (it
may be useful to look in an elementary statistics book) and the key to the
solution will be to find the probability that no nucleation event
occurs in the time-cone for a point ![]() .
.
Poisson statistics apply when events are random and mutually independent,
which is assumed to be the case both in time and along the wire.1Therefore, the problem depends only on the area of the time cone
illustrated
for the three distinct cases for
![]() .
.