Last time

Heterogeneous Nucleation

Decomposition versus Order/Disorder Kinetics

Simulations on a Square Lattice

3.21 Spring 2001: Lecture 33

Macroscopic Theories for Decomposition and Order/Disorder Kinetics

Background: Changes in Density of Extensive Functions for Conserved and Non-Conserved Quantities

Figure 33-1: Illustration of the change in molar free energy from a composition $c_0$. If the system is closed so the composition is fixed, then the change in any molar extensive quantity (e.g. molar free energy) is $\Delta \overline{F}_c$ for every mole which forms at composition $c'$. If the system is open and the composition is free to change its value--or if the quantity associated with the transformation is non-conserved, then $\Delta \overline{F}_u$ is the change per mole transformed.

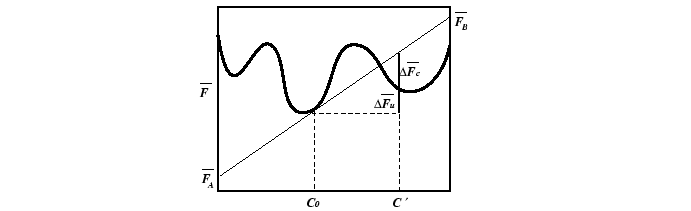Results for Small Variations

• Non-conserved quantities: If $\eta$ is a non-conserved quantity, like spin, or crystalline order, then for small changes in $\eta$ given by $\delta \eta$:

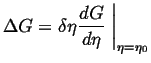  $$\Delta {G} = \delta \eta \frac{d {G}}{d\eta} \ensuremath{\left.\mbox{\rule{0pt}{16pt}}\right\vert}_{\eta = \eta_0}$$ (33-1)

  
  

  Therefore, an order parameter can always decrease the free energy by picking a variation $\delta \eta$ with a sign that makes the product in Eq. 33-1 negative. An non-conserved order parameter has no barrier against reaching a value which makes the free energy a local minimum.

  
  

• Conserved quantities: If $c$ is a non-conserved quantity, like concentration, then for small changes in $c$ given by $\delta c$:

  $$\Delta {G} = \frac{1}{2} (\delta c)^2 \frac{d^2 {G}}{dc^2} \ensuremath{\left.\mbox{\rule{0pt}{16pt}}\right\vert}_{c = c_0}$$ (33-2)

  
  

  Therefore, a barrier to the growth of small variations exists whenever the second derivative in Eq. 33-2 is positive. Thus, nucleation is required for a transformation outside of the spinodal curves.

  In fact, it can be shown that the sign of the diffusivity, $D$, for concentration flux is given by the second derivative ${\partial^2 {G}}/{\partial c^2}$. This has the effect of causing ``up-hill'' diffusion.

  
  

Macroscopic Theories for Decomposition Kinetics

It is possible, but currently impractical, to model the kinetics of an order/disorder reaction or a spinodal decomposition by simulating the motions of individual atoms. In this section, a coarse-graining procedure is developed and partial differential equations are developed for the evolution of the coarse-grained parameters.¹

Figure 33-2: Illustration of order parameter fields in the diffuse interface theories. The concentration field is a continuum limit of a concentration variable at each point in the material--similar constructions can be applied to order parameters. For example, $\eta (x)$, may represent the magnetic spin density in a material that is understood to be a continuum limit of spins on a lattice.

It is possible to derive the kinetics of order/disorder and spinodal decomposition from the same underlying principles. In the case of spinodal decomposition, extra considerations for the locally conserved composition field will result in a different kinetic relation.

Let $y(\vec{x})$ represent either a conserved or non-conserved quantity, and consider how an arbitrary distribution $y(\vec{x})$ evolves towards equilibrium.

We will take a variational calculus approach of writing down an expression for the total free energy in terms of $y$ and its gradients.

The total free energy of the entire system (occupying the domain $\Omega$) is:

$$F[y(x)] = \int_\Omega ( f(y) + \frac{K}{2} \nabla y \cdot \nabla y) dV$$ (33-3)

which defines $F$ as a functional with the argument $y(\vec{x})$². The function $y(\vec{x})$ will also have specified boundary conditions on $\partial \Omega$ (the boundary of $\Omega$); for instance, $y(\partial \Omega)$ will have fixed values or fixed derivatives.

If the field $y(\vec{x})$ is changing with velocity $v(\vec{x})$, the is the rate of change of $F$ is

$$F(y + vt) = \int_\Omega [ f(y+ vt) + + \frac{K}{2} ( \nabla y \cdot \nabla y + 2 t \nabla y \cdot \nabla v + t^2 \nabla v \cdot \nabla v ] dV$$ (33-4)

and it can be shown³

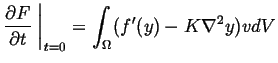$$\frac{\partial F}{\partial t} \ensuremath{\left.\mbox{\rule{0pt}{16pt}}\right\vert}_{t=0} = \int_\Omega ( f'(y) - K \nabla^2 y ) v dV$$ (33-5)

The change in total energy in Eq. 33-5 is the sum of local variations: $( f'(y) - K \nabla^2 y ) v$. Therefore, the largest possible increase of $F$ is when the flow, $v(\vec{x})$ is proportional to (minus) the other factor in the integrand of Eq. 33-5:

$$v(\vec{x}) = -M f'(y) - K \nabla^2 y$$ (33-6)

Therefore, The right-hand-side of Eq. 33-6 is the functional gradient of $F(y)$ and can be associated with the local potential for changing the field $y$ so as to reduce the total energy $F[y]$.

The functional gradient is the starting point for the kinetic equations for conserved and non-conserved parameter fields.

Kinetics of Non-conserved Order Parameters:
The Allen-Cahn Equation

For a non-conserved order parameter $\eta(\vec{x})$, Eq. 33-6 is the local rate of increase of free energy for a small change $\delta \eta(\vec{x})$; therefore $-(f'(\eta) - K_\eta \nabla^2 \eta)$ is the driving force to change $\eta$. No long-range diffusion is required (in other words, the order parameter can change with no flux of order into an element $dV$). Therefore, assuming kinetics that are linear in the driving force:

$$\frac{\partial \eta}{\partial t} = M_\eta [K_\eta \nabla^2 \eta - f'(\eta)]$$ (33-7)

which is known as the Allen-Cahn equation for describing order-disorder kinetics. It is also called Model A or the non-conserved Ginsberg-Landau equation.

Allen-Cahn: Critical Microstructural Wavelengths

Consider a system where $f(\eta)$ has two minima at $\eta = \pm 1$:

$$f(\eta) = f_s ((1+\eta)(1-\eta))^2$$ (33-8)

where $f_s$ is the height at the unstable saddle point at $\eta=0$. Suppose the system is initially uniform at unstable point $\eta=0$ (for instance, the system may have been quenched from a higher temperature, disordered state and $\eta = \pm 1$ represent two equivalent ordering variants). If the system is perturbed a small amount by a planar perturbation in the $z$-direction, $\eta(\vec{x}) = \delta(t) \sin(\omega z)$. Putting this and Eq. 33-8 into Eq. 33-7, and keeping the lowest order terms in $\delta(t)$:

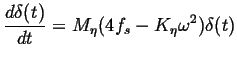$$\frac{d \delta(t)}{dt} = M_\eta ( 4 f_s - K_\eta \omega^2) \delta(t)$$ (33-9)

so that

$$\delta(t) = \delta(0) \exp[ M_\eta ( 4 f_s - K_\eta \omega^2 )t]$$ (33-10)

The perturbations grow if

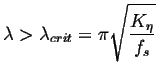$$\lambda > \lambda_{crit} = \pi \sqrt{\frac{K_\eta}{f_s}}$$ (33-11)

which is approximately equal to the interface width.

Note that the amplification factor is a weakly increasing function of wavelength (asymptotically approaching $4 M_\eta f_s$ at long wavelengths). This would predict that the longest wavelengths would dominate the morphology of an order-disorder phase transition. However, the probability of finding a long wavelength perturbation is a decreasing function of wavelength and this also has an effect on morphology.

The Kinetics of Conserved Parameters:
The Cahn-Hilliard Equation

Because $c(x)$ is a (locally) conserved parameter, the flux of $c$ from one volume element to its neighbor will affect the kinetics. $c(\vec{x})$ is guaranteed to be conserved if $\partial c/\partial t$ is the divergence of a flux.

Equation 33-6 is the local increase of free energy density due to a local addition $\delta c(\vec{x})$. The flux is assumed to be linear in the gradient of Eq. 33-6:

$$\vec{J}_c = -M_c \nabla [ f'(c(\vec{x})) - K_c \nabla^2 c]$$ (33-12)

This is equivalent to the linear assumption in Fick's law. The proportionality factor $M_c$ is related to the interdiffusion coefficient. However, $M_c$ is necessarily positive.

Therefore, the local rate of increase of the composition is given by (minus) the divergence of the flux:

$$\frac{\partial c}{\partial t} = \nabla \cdot M_c \nabla [ f'(c(\vec{x})) - K_c \nabla^2 c(\vec{x})]$$ (33-13)

if $M_c$ is constant, then

$$\frac{\partial c}{\partial t} = M_c [\nabla^2 f'(c(\vec{x})) - K_c \nabla^4 c(\vec{x})]$$ (33-14)

which is known as the Cahn-Hilliard equation describing the kinetics of spinodal decomposition. It is also called Model B or the conserved Ginsberg-Landau equation.

The first term on the right-hand side of Eq. 33-14 looks like the classical diffusion equation in regions where $f(c)$ can be reasonably approximated by a quadratic function, (for instance near the minima of $f$). The fourth-order term has the effect of stabilizing the shortest wavelengths when $f''< 0$, as discussed below.

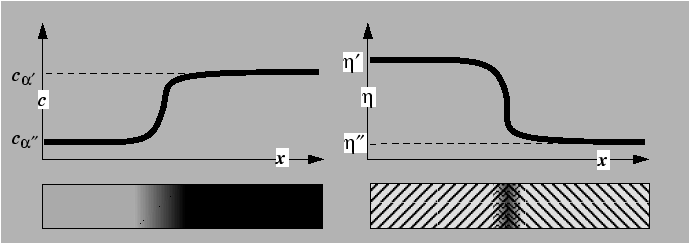
Cahn-Hilliard: Critical and Kinetic Wavelengths

Consider the following function as an approximation to the regular solution model:

$$f(c) = \frac{16 f_s}{(c_\beta - c_\alpha)^4} [ (c - c_\alpha)(c - c_\beta) ]^2$$ (33-15)

which has minima at concentrations $c_\alpha$ and $c_\beta$ and a maximum of height $f_s$ at $c = c_{avg} \equiv (c_\alpha + c_\beta)/2$. Suppose we have an initially uniform solution at $c = c_{avg}$ and that we perturb the concentration with a small plane wave: $c(\vec{x}) = c_{avg} + \epsilon(t) \sin \omega z$. Putting this into Eq. 33-14 and keeping the lowest-order terms in $\epsilon(t)$,

$$\frac{d \epsilon}{dt} = \frac{M_c \omega^2}{(c_\beta - c_\alpha)^2} [16 f_s - K_c \omega^2(c_\beta - c_\alpha)^2] \epsilon$$ (33-16)

Therefore any wavelength $\lambda$ will grow if

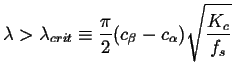$$\lambda > \lambda_{crit} \equiv \frac{\pi}{2} (c_\beta - c_\alpha) \sqrt{\frac{K_c}{f_s}}$$ (33-17)

Taking the derivative of the amplification factor in Eq. 33-16 with respect to $\omega$ and setting it equal to zero, we find the fastest growing wavelength:

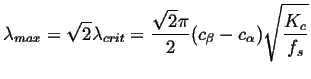$$\lambda_{max} = \sqrt{2} \lambda_{crit} = \frac{\sqrt{2}\pi}{2} (c_\beta - c_\alpha) \sqrt{\frac{K_c}{f_s}}$$ (33-18)

It is expected that domain size in the early stage of spinodal decomposition will be approximately $\lambda_{max}$.

Note that this approach for conserved order parameter is analogous to the case of kinetic and thermodynamic stability of a cylinder with axial perturbations:

Figure 33-3: The amplification factor for spinodal decomposition and order-disorder reactions.

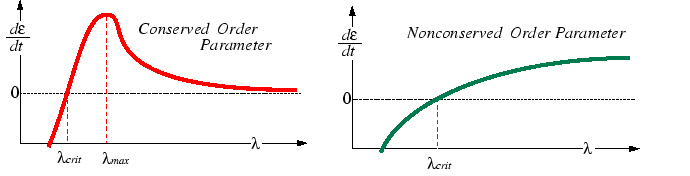Simulations

Below are simulations of Eqs. 33-7 and 33-14 with initial conditions taken as a small perturbation about the unstable (or saddle) point.

Can you determine, by observation, which simulation corresponds to which type of kinetics?

Figure 33-4: A simulation-can you determine which type of kinetics? If you are viewing in HTML, click on the figure to see the simulation.

Figure 33-5: A simulation-can you determine which type of kinetics? If you are viewing in HTML, click on the figure to see the simulation.

• About this document ...