Last time: Spinodal decomposition--III; Nucleation--I.

Spinodal microstructures

Later stages

Nucleation theory: Introductory concepts

• Driving forces and resisting forces

• $\Delta G_{c}$ for homogeneous nucleation

Today: Nucleation--II.

Role of elastic strain energy in nucleation

Theory for steady-state nucleation rate

Heterogeneous Nucleation

3.21 Spring 2001: Lecture 31

Nucleation theory--II.

Role of elastic strain energy

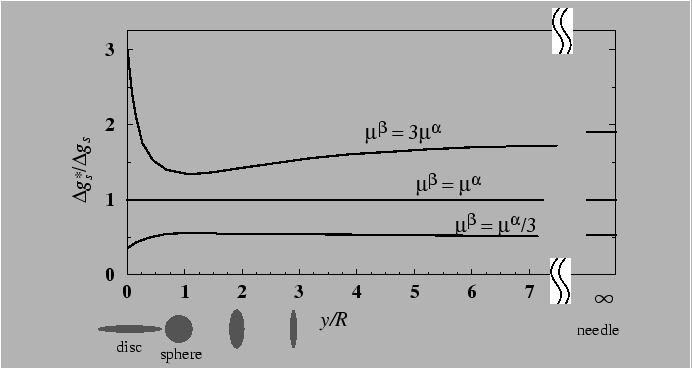
In supersaturated crystalline solid solutions the first particles of the new phase that form are generally coherent with the matrix, because of the lower interphase boundary energy relative to semicoherent or incoherent interfaces. However, coherent inclusions have an associated elastic strain energy that resists nucleation. This elastic strain energy is not easy to express with simple algegraic expressions, except for particularly ideal cases.

If nucleation of an incoherent particle were to occur, it would do so without attendant elastic strain energy, because the incoherent interface would act as a perfect source or sink of point defects and the successful critical nucleus, with the lowest $\Delta Gc$, would be a configuration without the energy penalty of elastic strain energy.

The method for calculating the elastic strain energy of coherent inclusions was developed most elegantly by J.D. Eshelby, and it uses an idealized procedure to create the inclusion and calculate the accompanying strain energy. Eshelby's procedure consists of four steps:

1. Excise region to be transformed from matrix

2. Alloy excised region to undergo stress-free transformation strain $\epsilon_{ij}^{T}$.

3. Apply surface tractions to particle to restore if to its untransformed shape.

4. Place particle back into matrix, specify boundary conditions appropriate to state of coherency, and allow particle/matrix system to relax.

The easiest class of problems of this type to solve make these assumptions: elastic isotropy, elastic homogeneity (same elastic constants in particle and matrix), and that the particle shape is an ellipsoid of revolution (semiaxes $a$, $b$, and $c$). Thus, the theory allows for a particle-shape dependence of elastic strain energy.

Two cases: Pure dilatational transformation; pure shear transformation

Figure 31-1: Effect of elastic heterogeneity on elastic strain energy of coherent ellipsoidal inclusion vs. aspect ratio $y/R$. Particle and matrix are isotropic.

Nucleation kinetics

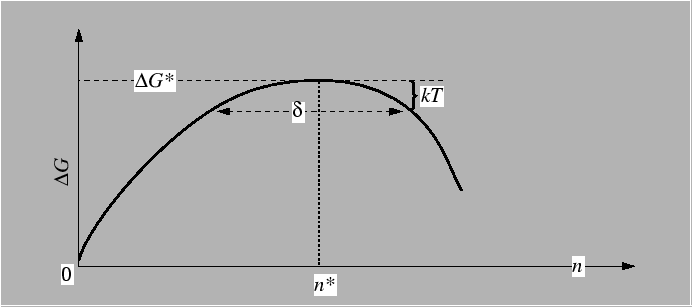
Equilibrium distribution of clusters. Effect of losing clusters at sizes greater than critical sizes. Concept of "diffusion equation" for steady-state distribution when clusters greater than critical size are being lost.

Key results:

$$J = Z \beta_c N \exp \left( \frac{- \Delta G_c}{kT} \right)$$ (31-1)

where

$$Z \equiv \sqrt{\frac{\Delta G_c}{3 \pi n_c^2 kT}}$$ (31-2)

Time-dependent nucleation

Figure 31-2: Variation of free energy with size of fluctuation in the nucleation regime. The curvature at the top of the barrier determines the time for clusters to "random walk" over the barrier and thus influences the relaxation time $\tau$ for transient nucleation kinetics.

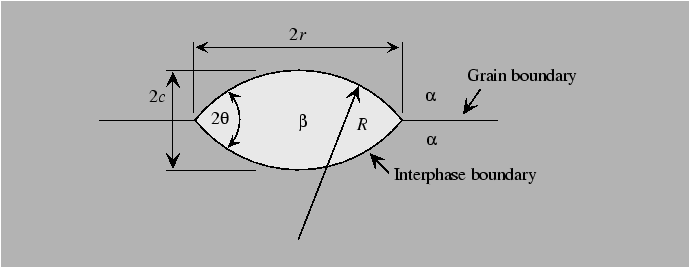
Heterogeneous nucleation

Heterogeneous nucleation can occur on imperfections when the nucleating particle effectively "replaces" some energetic feature of the original configuration. For instance, nucleation on a grain boundary removes grain boundary area and replaces it with interphase boundary area that would have been created anyway by formation of the new phase. Thus, prexisting imperfections effectively "catalyze" the nucleation process. We'll consider the case of heterogeneous nucleation on grain boundaries.

Figure 31-3: Geometrical parameters defining size and shape of a lenticular $\beta$ particle situated on a grain boundary in phase $\alpha$.

Key results:

1. $R_{c}$ is the same as for homogeneous nucleation.

2. $\Delta G_{c}$ is reduced proportionally to the volume reduction of the critical nucleus.

3. The heterogeneous nucleation kinetics will be influenced by both the reduction in $\Delta G_{c}$ (which favors heterogeneous nucleation) and by the number of sites available for heterogeneous nucleation (which favors homogeneous nucleation. These two competing factors can be sorted out by working through the equations and using a model for the dependence of the number os sites available for heterogeneous nucleation on the microstructure (e.g., grain size for heterogeneous nucleation on grain boundaries). Details are given in Section 23.3 in the notes.