Last time: Spinodal decomposition--II.

Gradient energy

Elastic energy

Improved diffusion equation

• Modification to Fick's laws

• Solution to diffusion equation

• Spinodal microstructures

• Later stages of spinodal decomposition

Today: Spinodal decomposition--III; Nucleation--I.

Spinodal microstructures

Later stages

Nucleation theory: Homogeneous

• Theory of steady-state nucleation

• Transient nucleation

• Role of elastic strain energy in nucleation

The solution to the linearized diffusion equation that includes gradient-energy effects has as its key feature an exponential growth of composition waves over a range of wavenumbers $\beta$ inside the coherent spinodal. One wavenumber, $\beta_m$, receives the maximum amplification. The theory predicts that the evolving microstructure of growing waves will quickly become dominated by waves with wavenmubers near $\beta_m$. So one key aspect of spinodal microstructures is spatial periodicity.

In crystalline solutions, two additional points are important. First, at the early stages of decomposition, spinodal microstructures are always fully coherent and they can develop only within the coherent spinodal. Second, if the solution is elastically anisotropic, the wavevectors of the dominant waves will be aligned along elastically soft directions in the material. In cubic crystals, the <100> directions are usually the elastically soft directions .

Hence, in crystalline solutions, spinodal microstructures usually show both periodicity and alignment.

The kinetics of spinodal decomposition is usually studied by small-angle scattering techniques (light, x-rays, or neutrons). Spinodal microstructures in solids usually involve decomposition wavelengths on the order of 2-50 nm, so high-resolution imaging techniques like transmission electron microscopy or field-ion microscopy are employed.

The following images are typical of spinodal microstructures in metals and show examples of decomposition in elastically isotropic (Fe-Cr-Co) and anisotropic (Fe-Be) alloys imaged by field-ion microscopy. Images reproduced from S.S. Brenner, P.P. Camus, M.K. Miller, and W.A, Soffa, Acta metall. 32, 1217-1227 (1984).

Figure 30-1: Spinodal microstructures observed by atom-probe field-ion microscope. (a) isotropic structure in Fe-Cr-Co aged at 600°C for 8 h. (b) Aligned structure in Fe-Be aged at 400°C for 20 nmin. (Brenner et al., 1984.)

Later stages of spinodal decomposition

The linearized diffusion equation ignores several factors that limit the validity of its solution for all but the shortest decompostion times. One obvious deficiency is the assumption that $f\prime\prime$ is constant. This means that the decomposition can only be valid for equal volume fractions of both phases, and also that the composition amplitude will grow without limit. An additional freature missing in the theory is interactions between growing waves, and these interactions lead to gradual coarsening of the evolving two phase structure. Most spinodal transformations observed experimentally show increasing characteristic wavelengths with decomposition time, from the earliest stages of the transformation. These nonlinear effects are discussed in considerable detail in Cahn 1966.

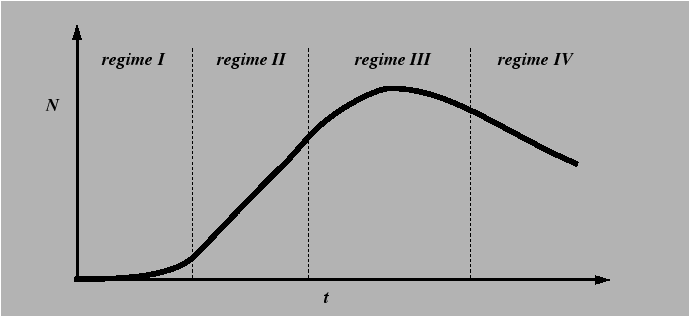
Nucleation theory: Homogeneous

Figure 30-2: Number of particles, $N$, vs. time $t$ during a precipitation reaction from the nucleation to the coarsening regimes.

Theory of steady-state nucleation

$$\Delta G_n=n(\mu _\beta -\mu _\alpha )+\eta n^{2/3}\ensuremath{\gamma}$$ (30-1)

Figure 30-3: Bulk and interfacial free energy vs. size $n$ in the nucleation regime. The maximum in $\Delta G_n$ defines the critical size $n_c$

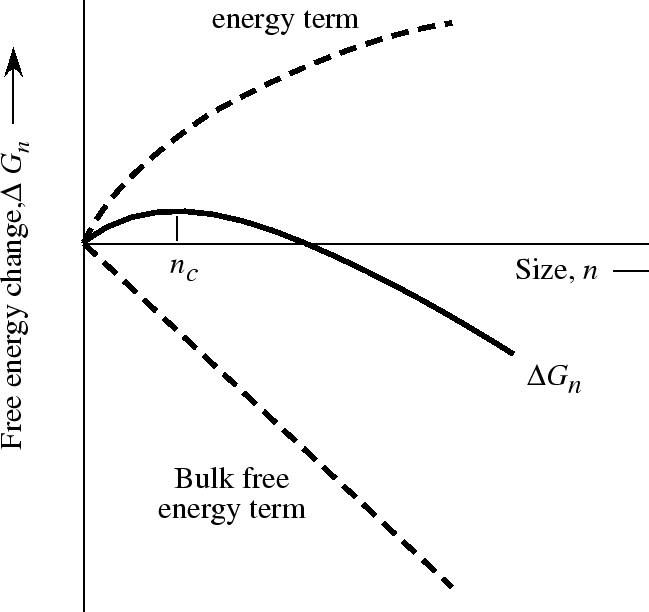A theory for the steady-state nucleation regime must account for the equilibrium distribution of clusters of size $n$ present in the supersaturated solution. Fluxes in size-distribution space near the critical size $n_c$ can be used to develop a simple expression for the steady-state nucleation rate.

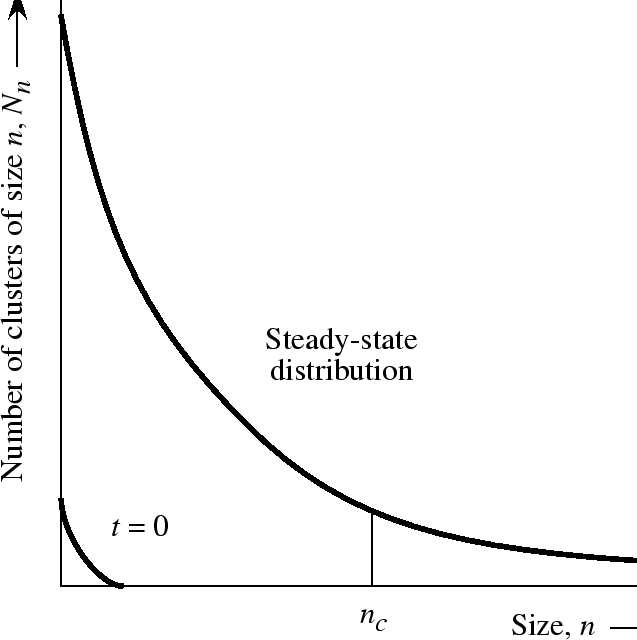
Time-dependent nucleation

Figure 30-4: Schematic illustration of the variation of the cluster size distribution at two different times in the transient regime.

Elastic strain energy effects on nucleation in solids

Interface structure, energy, and strain energy of inclusions

Figure 30-5: Interfacial structure for (a) coherent and (b) semicoherent interfaces between matrix phase $\alpha$ and particle phase $\beta$. Smaller dislocation symbols represent coherency dislocations and larger ones in (b) represent anticoherency dislocations.

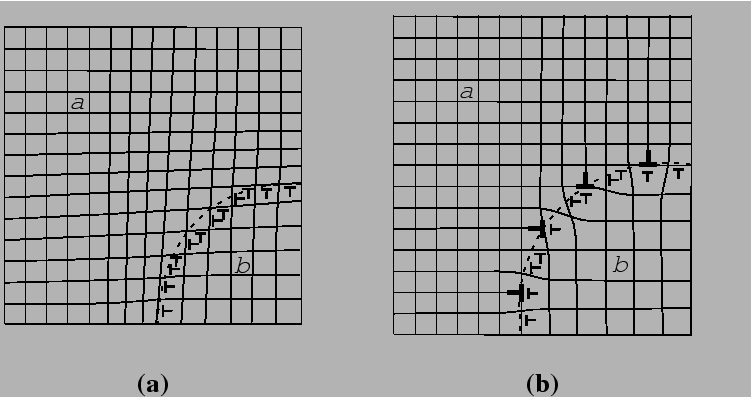Eshelby's method for calculating the elastic strain energy of coherent inclusions; some simple cases.