Last time: Particle coarsening.--II
Elements of mean-field theory for DCC
Complications of real systems
Experimental study of coarsening in semi-solid Pb-Sn alloys (Hardy and Voorhees 1988
Today: Phase Transformations: Overview
Metastability, instability, and mechanisms
First-order and second-order transitions
Free energy functions; conserved and nonconserved variables
Spinodal decomposition--I.
Phase Transformations: Overview
Metastability, instability, and mechanisms
A phase transformation can occur when a system has an accessible state of lower free energy. The mechanism of the transformation is critically dependent on whether the starting state is metastable or unstable.
An unstable system can transform by making changes that are small in degree but large in extent. Such situations lead to mechanisms that are called continuous transformations. The main categories of continuous transformations in materials are spinodal decomposition and continuous ordering.
A metastable system can transform by making changes that are large in degree but small in extent. Such situations require nucleation of the new phase. After nucleation takes place, a new particle can grow until it either impinges with another particle, or supersaturation of the surrounding material is depleted.
First-order and second-order transitions
Ehrenfest proposed a useful scheme for classification of phase
transformations based on discontinuities in derivatives of the free
energy function ![]() that are characteristic of the transformation.
Simply put, the order or a phase transformation is the lowest
order of the derivative of
that are characteristic of the transformation.
Simply put, the order or a phase transformation is the lowest
order of the derivative of ![]() that shows a discontinuity.
that shows a discontinuity.
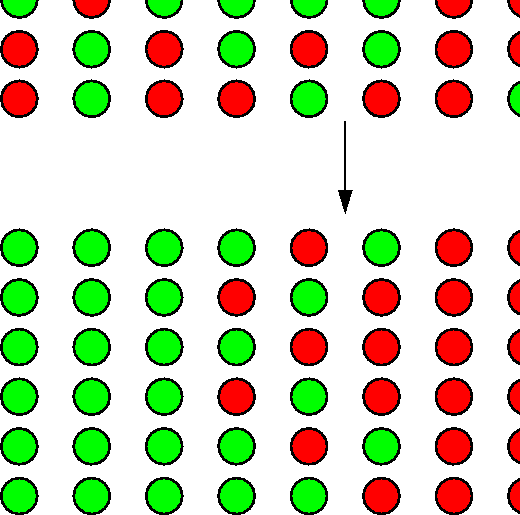
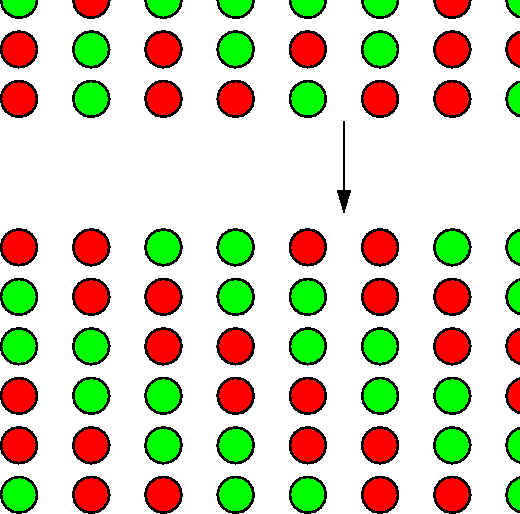
Examples: melting; ordering in ![]() brass
brass
 |
 |
Order Parameters and Phase Transformations
Consider a simple one component phase transformation:
We can express the transformation near the transition as a Landau expansion
| (27-1) |
where ![]() might be some measure of a ``hidden parameter'' such as
the diffuseness of a peak in the atomic radial-distribution function.
might be some measure of a ``hidden parameter'' such as
the diffuseness of a peak in the atomic radial-distribution function.
The equilibrium value of ![]() is given by
is given by
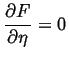 |
(27-2) |
We will use functions like ![]() to follow evolution towards
equilibrium values
to follow evolution towards
equilibrium values
![]() .
.
Spinodal decomposition
The chemical spinodal and "uphill diffusion"
Recall that
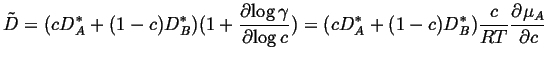 |
(27-3) |
Note that since,
![]() , that the
diffusivity has the same sign as the second derivative of the
free energy:
, that the
diffusivity has the same sign as the second derivative of the
free energy:
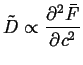 |
(27-4) |
Consider the following free-energy curve and resulting phase diagram:
In region III,
![]() , how does the diffusion equation behave
when
, how does the diffusion equation behave
when
![]() ? Recall that for initial conditions
? Recall that for initial conditions
![]() the diffusion equation has solution:
the diffusion equation has solution:
| (27-5) |
This will be very badly behaved for small wavelengths and give no end of trouble. It is ill-posed.
Gradient Energy
How to fix this problem and calculate a governing equation inside the spinodal region?
Consider the following profile or variation in field:
What kind of penalties can be imposed that ``mimic'' surface energy?
Should the penalty depend on the whether the field is increasing left-to-right or increasing right-to-left?
For inhomogenous fields, expand the free energy about its homogenous value:
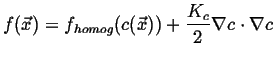 |
(27-6) |
![]() is the gradient energy coefficient, it introduces surface energy into the
free energy and will ``regularize'' the diffusion equation within
(and applies outside
as well) the spinodal.
is the gradient energy coefficient, it introduces surface energy into the
free energy and will ``regularize'' the diffusion equation within
(and applies outside
as well) the spinodal.
For one-dimensional variations, the free energy density is:
Theory of diffuse interfaces