 |
Last time
Homogeneous Nucleation: Simple Model
Steady-State Nucleation Rate
Nucleation Incubation Time
Further Considerations of Nucleation in Solids
The simple theory of nucleation that was developed above contained several assumptions that are inappropriate for nucleation of a solid nucleus in a solid matrix. The assumption of constant and isotropic surface tension is incompatible with many experimental observations in solids. When the nucleating phase has a different volume or shape than the matrix material that it replaces, elastic energy must be considered as part of the volumetric contribution to nucleation.
The interfacial contribution to the nucleation barrier dominates at small nucleus sizes and volumetric contributions dominate at large nucleus sizes. The competition between these contributions can produce a complicated sequence of states for a developing phase--at small nuclei, the system may select a state that minimizes surface energy at the expense of elastic contributions; at larger sizes, interfacial structure can change with concomitant increases in interfacial energy if such a change decreases the excess energy through the volumetric contributions. The sequence of states may include changes in interfacial structure that relax elastic energy or even phase changes in the nuclei if less stable phases have smaller interfacial energies.
Role of Interface Structure on Interfacial Energy
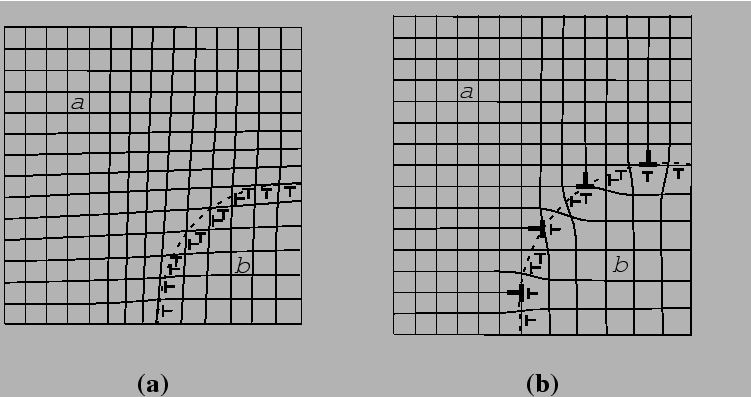
When the nucleating phase has a crystal structure that is the same as its parent phase but differ only in composition or stress-free strain (e.g., they might have different molar volume), a small nucleus can assume non-equilibrium compositions or strains that minimize energy by satisfying interfacial bonds at the expense of volumetric chemical or elastic energy.
Typically for solid-state nucleation, elastic energy considerations dominate at small particle sizes and the interfacial energy can be reduced significantly by adopting a coherent structure. As the particle grows, elastic energy can be reduced by the introduction of misfit dislocations into the interface. Such interface dislocations transform a coherent into a semi-coherent interface at the expense of increased interfacial energy.
 |
 |
When there is no long-range lattice matching across an interface, the interface is incoherent.
Role of Elastic Energy in Nucleation
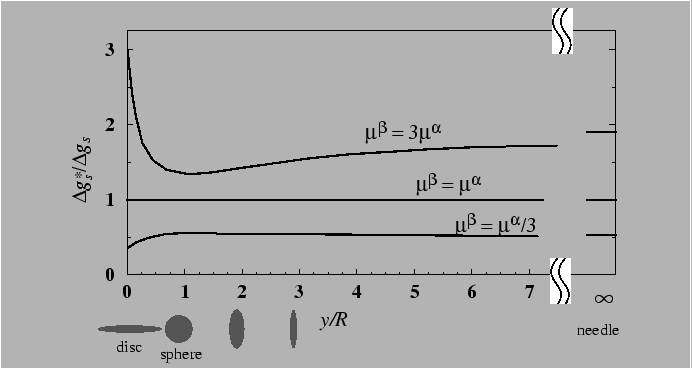
In supersaturated crystalline solid solutions the first particles of the new phase that form are generally coherent with the matrix, because of the lower interphase boundary energy relative to semicoherent or incoherent interfaces. However, coherent inclusions have an associated elastic strain energy that resists nucleation. This elastic strain energy is not easy to express with simple algebraic expressions, except for particularly ideal cases.
If nucleation of an incoherent particle were to occur, it
would do so without attendant elastic strain energy, because the
incoherent interface would act as a perfect source or sink of point
defects and the successful critical nucleus, with the lowest ![]() , would be a configuration without the energy penalty of elastic
strain energy.
, would be a configuration without the energy penalty of elastic
strain energy.
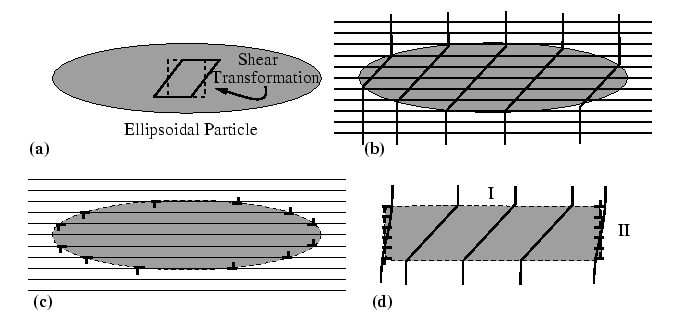
The method for calculating the elastic strain energy of coherent inclusions was developed most elegantly by J.D. Eshelby, and it uses an idealized procedure to create the inclusion and calculate the accompanying strain energy. Eshelby's procedure consists of four steps:
The easiest class of problems of this type to solve make these
assumptions: elastic isotropy, elastic homogeneity (same elastic
constants in particle and matrix), and that the particle shape is an
ellipsoid of revolution (semiaxes ![]() ,
, ![]() , and
, and ![]() ). Thus, the
theory allows for a particle-shape dependence of elastic strain
energy.
). Thus, the
theory allows for a particle-shape dependence of elastic strain
energy.
 |
Heterogeneous Nucleation
Heterogeneous nucleation can occur on imperfections when the nucleating particle effectively ``replaces'' some energetic feature of the original configuration. For instance, nucleation on a grain boundary removes grain boundary area and replaces it with interphase boundary area that would have been created anyway by formation of the new phase. Thus, preexisting imperfections effectively ``catalyze'' the nucleation process.
 |
Heterogeneous nucleation is a commonly observed phenomenon.
Question: How do you explain the following phenomena?
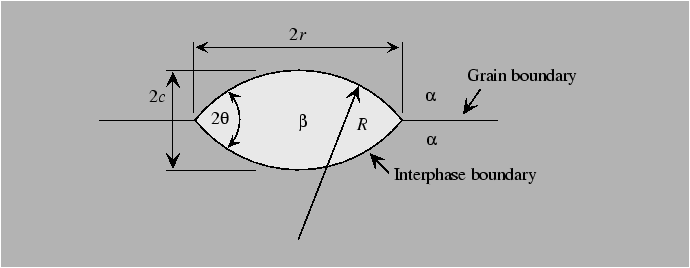
Heterogeneous nucleation can be understood by considerations of the geometry of the nucleus. A simple model for the case of nucleation of a new phase on an isotropic grain boundary can be obtained by assuming that the nuclei have the shape of two hemispherical caps that abut with an equilibrium dihedral angle given by the Young force balance equation. The model equations can be derived in a parallel to the critical spherical nucleus size that balanced the rate of volumetric energy decrease with the rate of interfacial energy increase.
The following results apply.
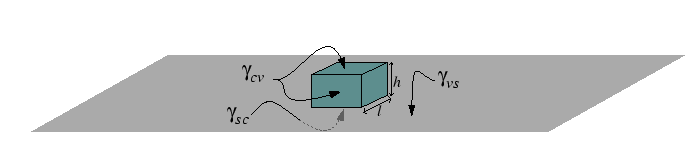
The steps can be illustrated for a highly anistropic
interface by a simple example of a cubic crystal with
![]() -facets nucleating in a
-facets nucleating in a ![]() -direction.
-direction.
 |
For this case, the ![]() for homogeneous nucleation is given by the maximum of
for homogeneous nucleation is given by the maximum of
| (25-1) |
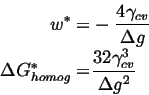 |
(25-2) |
For heterogeneous nucleation,
| (25-3) |
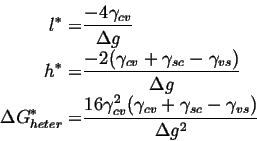 |
(25-4) |
The shape of the particle is determined by the differences in surface tensions and the geometrical factors associated with the shape of the particle determine the nucleation barrier for heterogeneous diffusion.
Nucleation on Dislocations
Dislocations provide sites of increased energy in a crystal where nucleation can be assisted by reduction of the core and elastic energy of a dislocation.
Location of Heterogenous Nucleation
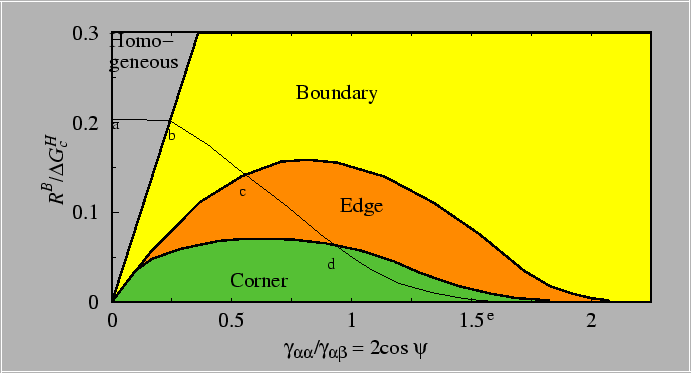
The heterogeneous nucleation kinetics will be influenced by both
the reduction in
![]() (which favors heterogeneous
nucleation) and by the number of sites available for heterogeneous
nucleation (which favors homogeneous nucleation. These two competing
factors can be sorted out by working through the equations and using
a model for the dependence of the number of sites available for
heterogeneous nucleation on the microstructure (e.g., grain size for
heterogeneous nucleation on grain boundaries).
(which favors heterogeneous
nucleation) and by the number of sites available for heterogeneous
nucleation (which favors homogeneous nucleation. These two competing
factors can be sorted out by working through the equations and using
a model for the dependence of the number of sites available for
heterogeneous nucleation on the microstructure (e.g., grain size for
heterogeneous nucleation on grain boundaries).
 |