 |
Last time
Diffusion as a sequence of Random Jumps
Diffusion as a time-dependent probabiltity distribution
Concentration as calcuated from Fick's law as a probability field
Mechanisms of Diffusion in Crystals
Ring Mechanism
Vacancy Mechanism
Interstitialcy Mechanism
Interstitials
Types of Interstitials
Simple Models for Interstitial Diffusivity
Recall that for a random walk in three-dimensions:
The reaction rate theory was worked out for the case of activation over a particular barrier, i.e.,
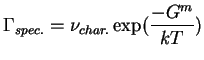 |
(16-2) |
The relation of
![]() to the total succesful hop frequency
is the sum of hop frequencies of all surrounding sites
to the total succesful hop frequency
is the sum of hop frequencies of all surrounding sites
where
![]() is the particular hop frequency into a site of type
is the particular hop frequency into a site of type ![]() and
and ![]() is the degeneracy (i.e., count) of similar neighbors.
is the degeneracy (i.e., count) of similar neighbors.
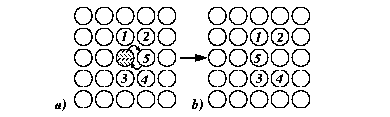
For example, consider the case of an interstitial atom in FCC-iron.
There are four crystallographically similar nearest interstitial sites (
![]() );
if the successful hop frequency into the next nearest neighbor,
);
if the successful hop frequency into the next nearest neighbor,
![]() , is
negligible compared to the nearest neighbor hops (
, is
negligible compared to the nearest neighbor hops (
![]() )
then
)
then
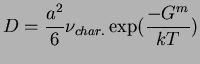 |
(16-5) |
The Gibbs free energy of the activated state in the exponent results from the caveat of fixed stress.
The Helmholtz free energy would appear for the case of fixed volume.
Hydrostatic stress is results from the assumption that each neighboring interstitial site is
the same--this would not be the case, for example, in tension
(
![]() and
and
![]() ).
Tension would break the symmetry of the interstitial sites by a tetrahedral distortion.
This effect has been observed in steel.
).
Tension would break the symmetry of the interstitial sites by a tetrahedral distortion.
This effect has been observed in steel.
Simple Models for Vacancy Diffusivity
The transition of an atom into a vacant site has the same treatment as the above case for interstitials, except that two additional factors must be considered:
The activation barrier, ![]() , depends on the presence of a neighboring vacancy.
The terms in the probabilities are not necessarily independent, but it is
a good approximation to treat the probabilities as independent terms so that
they multiply.
, depends on the presence of a neighboring vacancy.
The terms in the probabilities are not necessarily independent, but it is
a good approximation to treat the probabilities as independent terms so that
they multiply.
With the physically justifiable assumption that vacant site occupation is small (thus
neglecting the probability of two neighboring vacancies1, the successful hop frequency ![]() can be related to the
sum of particular vacancy hops as in equation 16-3.
can be related to the
sum of particular vacancy hops as in equation 16-3.
For self-diffusion on a hydrostatically stressed FCC lattice, there are 12 crystallographically
similar nearest neighbor sites,
![]() .
Therefore the successful hop frequency of an FCC-vacancy is:
.
Therefore the successful hop frequency of an FCC-vacancy is:
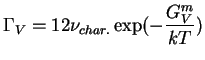 |
(16-6) |
Disregarding all other mechanisms of diffusion (i.e., interstiticialcy)
The successful hop frequency, ![]() of an atom chosen at random
is the product of two probabilities:
of an atom chosen at random
is the product of two probabilities:
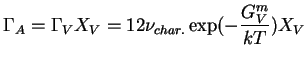 |
(16-7) |
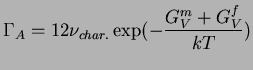 |
(16-8) |
Collecting terms and relating the jump distance, ![]() , to the lattice constant
, to the lattice constant
![]() ,
,
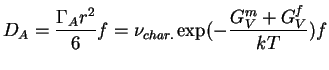 |
(16-9) |
Lattice Diffusion in Ionic Crystals
Just as in substitutional diffusion via the vacancy mechanism in which the diffusivity has an Arrhenius factor associated with the population of defects, a similar defect population appears in ionic crystals where the defects are more complicated.
In an ionic crystal, a vacancy at a cation (positive ion) or an anion site would leave a charge of the opposite sign unless that vacancy is compensated by another charged defect. The two common types of defects is a Schottky defect, where a pair of vacancies of opposite signs appear on each sublattice--and a Frenckel defect where a vacancy is compensated by an interstitial. If the cations and anions have differing magnitudes of ionic charge, then the defects must involve more sites to satisfy charge neutrality.
In ionic crystals, the notation for defect concentration identifies the chemical species, where the species is located relative to a perfect lattice, and the charge on the species. The commonly employed notation for charged defects is Kroger-Vink:
 |
(16-10) |
 |
(16-11) |
For example consider, putting calcia into a zirconia lattice:
CaO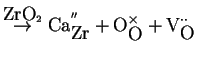 |
(16-12) |
The Schottky formation reaction is given by:
The equilibrium for Shottkey formation involves two unknowns:
Charge neutrality provides an additional constraint:
This forms a set of equations that can be solved for the
defect concentration that affects the diffusivity.