Next: About this document ...
Last Time
![]()
![]()
![]()
Next: About this document
...
Last Time
Solution Strategies
Brute Force: Numerical Methods
Diffusion with Moving Interfaces
Interface Motion due to Heat Absorption at the Interface
Mass Diffusion in an Alloy
Diffusion as a Molecular Process
The derivation of the diffusion equation followed from consideration of a continuum distribution of conserved particles. A treatment of individual molecular or atomic motions as part of a statistical ensemble of diffusing particles will prove to be not only consistent with the continuum approach, but will provide new physical concepts that enhance understanding of diffusive processes.
Below, the fundamental diffusive process--an atomic or molecular
displacement--is treated as a random jump occurring with an average
frequency ![]() .
It is instructive to consider how this simple model of random atomic
jumps corresponds to the various diffusion systems, or diffusivities
discussed above.
.
It is instructive to consider how this simple model of random atomic
jumps corresponds to the various diffusion systems, or diffusivities
discussed above.
First of all, if a jump is truly random, then the probability of a
given jump giving a net displacement ![]() must be exactly the same as jump with displacement
must be exactly the same as jump with displacement
![]() .
Therefore, the expected displacement,
.
Therefore, the expected displacement,
![]() ,
of a particle after one or more jumps must be identically zero.
Furthermore, the expected velocity of the particle,
,
of a particle after one or more jumps must be identically zero.
Furthermore, the expected velocity of the particle,
![]() ,
must also be zero. Considering the Einstein drift equation
,
must also be zero. Considering the Einstein drift equation
![]() ,
it must be concluded that the random walk treatment corresponds to the
physical experiment that
,
it must be concluded that the random walk treatment corresponds to the
physical experiment that ![]() ,
which is precisely the case that is intended for the measurement of the
self-diffusivity
,
which is precisely the case that is intended for the measurement of the
self-diffusivity ![]() ;
i.e. a diffusion couple of two alloys of the same composition, but
differing in isotopic concentration.
;
i.e. a diffusion couple of two alloys of the same composition, but
differing in isotopic concentration.
Secondly, if the jumps are assumed to take place on a crystalline
lattice, then each random displacement ![]() will be selected from a small subset of all the possible displacements
that would be available in the more general case of diffusion in a gas.
Treating the general case first, as is done below, leaves the diffusion
on the lattice as particular case.
will be selected from a small subset of all the possible displacements
that would be available in the more general case of diffusion in a gas.
Treating the general case first, as is done below, leaves the diffusion
on the lattice as particular case.
Third, for a process to be completely random, there can be no restriction on the availability of a nearby empty site--the probability of an empty site cannot appear in the simple model of random walk. In the simple random walk process, two atoms may occupy the same space. Therefore, the simple random walk treatment should not correspond to substitutional diffusion on a crystal lattice. However, substitutional crystalline diffusion can be treated as a sequence of random hops on a lattice if the ``particle'' that hops is one of a infinitely dilute concentration of vacancies-a vacancy will always have an occupied neighboring site to hop into in the dilute limit.
In the treatment of the random walk, the average rate at which a walker (i.e. an atom or molecule) takes steps is an empirical frequency
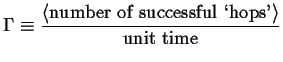 |
(13-1) |
A model for ![]() will be considered after the treatment of random walks and it will be
shown to depend on both a fundamental atomic rate at which an atom
attempts a hop, multiplied by the probability of success.
will be considered after the treatment of random walks and it will be
shown to depend on both a fundamental atomic rate at which an atom
attempts a hop, multiplied by the probability of success.
Diffusion as a Random Walk Process
Let ![]() be
the average rate that a random walker (an atom or molecule) `take
steps.'
be
the average rate that a random walker (an atom or molecule) `take
steps.' ![]() is
an average frequency.
is
an average frequency. ![]() be the position of a particular random walker:
be the position of a particular random walker:

|
The position of a particular particle (relative to the starting position) after a time
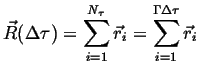 |
(13-2) |
What is meant by a ``random jump'' is not specified, but could be represented by a number of different processes:
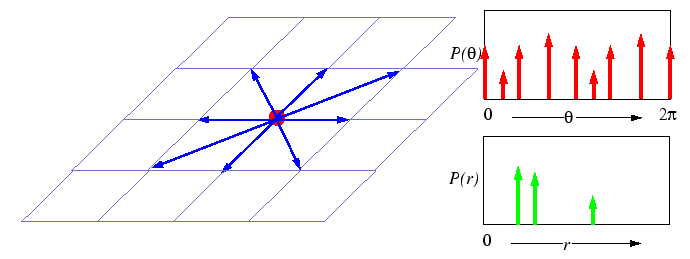 |
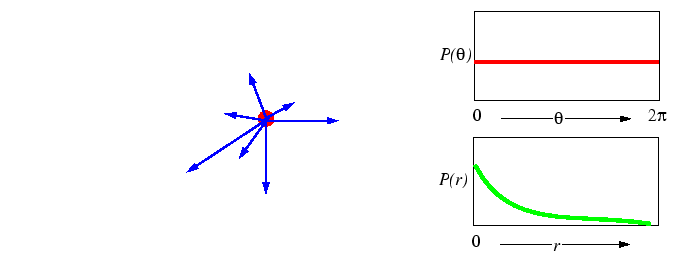 |
In either case, the expected value ![]() ;
this is an indication that no particular direction is favored and that
the driving force
;
this is an indication that no particular direction is favored and that
the driving force ![]() for a random walk.
for a random walk.
However, it should be intuitively clear that the distance between two
particles should increase with time. This distance is measured by the
spread, or second moment, of the distribution ![]() :
:
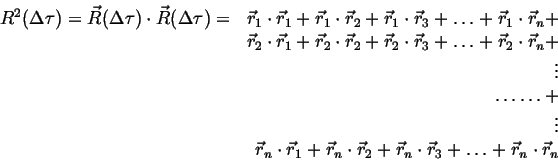 |
(13-3) |
This can be rewritten as a sum along the diagonal and off-diagonal terms:
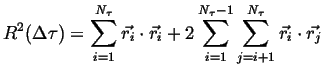 |
(13-4) |
Using the relationship ![]() ,
where
,
where ![]() is the angle between the
is the angle between the ![]() and
and ![]() jump-vectors. Therefore,
jump-vectors. Therefore,
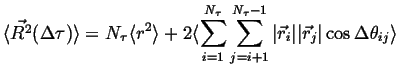 |
(13-5) |
Because ![]() ,
,
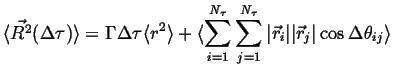 |
(13-6) |
No assumption about jump correlations, jump lengths, distribution of
values ![]() ,
or the number of dimensions has been made.
,
or the number of dimensions has been made.
If the lengths of the jumps do not correlate to the jump-angles:
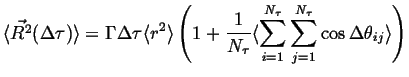 |
(13-7) |
where ![]() and
and ![]() have been factored out of both terms.
have been factored out of both terms.
Define the Correlation Factor, ![]() :
:
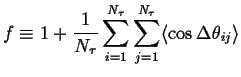 |
(13-8) |
Therefore,
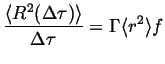 |
(13-9) |
This is an important equation, it relates the spread of the expected
square displacements (or the second moment of the probability
distribution) per unit time with three factors that are dictated by the
mechanism of diffusion: the rate of successful hops ![]() ,
the average square hop distance
,
the average square hop distance
![]() ,
and a factor related to the correlation between hops,
,
and a factor related to the correlation between hops, ![]() .
If every hop is uncorrelated and the probability of positive
displacement
.
If every hop is uncorrelated and the probability of positive
displacement ![]() is exactly balanced by an equal probability
is exactly balanced by an equal probability ![]() then
then ![]() .
.
If, in addition the jumps take place on a lattice with first neighbors only, and all the jumps are uncorrelated, then it can be shown that
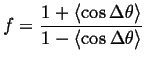 |
(13-10) |
Diffusion as a Time-Dependent Probability Distribution
In the last section, the expected position and the expected square
displacement of a particle was calculated by considering the statistics
of a sequence of random jumps. The concept of statistics can be coupled
with that of a probability distribution. The probability of finding a
particle after a time ![]() will be determined and will be related to the form of a point source
solution of the diffusion equation.
will be determined and will be related to the form of a point source
solution of the diffusion equation.
Consider a sequence of ![]() random jumps on a one-dimensional lattice. If the random walker is at
position
random jumps on a one-dimensional lattice. If the random walker is at
position ![]() after
after ![]() jumps (after starting at
jumps (after starting at ![]() ),
then the number of jumps to the right
),
then the number of jumps to the right ![]() and to the left
and to the left ![]() must satisfy:
must satisfy:
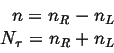 |
(13-11) |
The number of different ways that a random jumper could land at site ![]() from the origin is given by the binomial coefficient:
from the origin is given by the binomial coefficient:
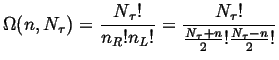 |
(13-12) |
Therefore the probability of getting to site ![]() after
after ![]() jumps is:
jumps is:
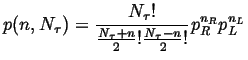 |
(13-13) |
If the probability of jumping right ![]() the probability of jumping left, then
the probability of jumping left, then
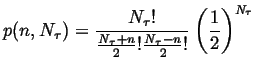 |
(13-14) |
Using Stirling's formula,
| (13-15) |
and taking the limit ![]() ,
,
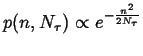 |
(13-16) |
which shows that the distribution of a point source in one dimension spreads as a Gaussian.
Using ![]() and
and ![]() :
:
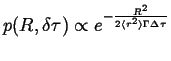 |
(13-17) |
Normalizing so that for all ![]()
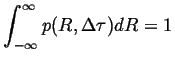 |
(13-18) |
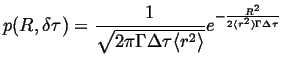 |
(13-19) |
Comparing this with the fundamental point solution in 1D:
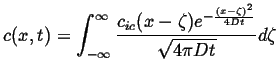 |
(13-20) |
The probability distribution can be used to identify the diffusivity with a random process:
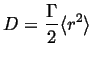 |
(13-21) |
for uncorrelated jumps (![]() )
on a one-dimensional lattice.
)
on a one-dimensional lattice.
Relation of the Self-Diffusivity to a Random Walk
The notion of the continuum limit for the concentration, ![]() of particles is consistent with an interpretation of the concentration
related to a probability of finding a particle of a given type within a
small distance of the point
of particles is consistent with an interpretation of the concentration
related to a probability of finding a particle of a given type within a
small distance of the point ![]() at a time
at a time ![]() .
Treating the concentration as a probability distribution, the second
moment of the distribution is related to the mean-square displacement
from the average displacement:
.
Treating the concentration as a probability distribution, the second
moment of the distribution is related to the mean-square displacement
from the average displacement:
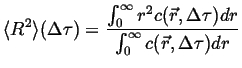 |
(13-22) |
Suppose all of the particles are located at the origin at time ![]() ,
then if diffusion takes place in three dimensions:
,
then if diffusion takes place in three dimensions:
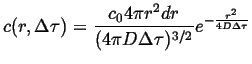 |
(13-23) |
Because,1
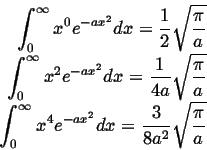 |
(13-24) |
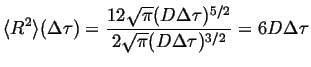 |
(13-25) |
Comparing this to Equation 13-9,
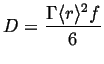 |
(13-26) |
This relates the macroscopic self-diffusivity to the jump frequency, average hop distance and correlation factor in three dimensions.
Using the point source in two dimensions, the analogous result for diffusion in one dimension is:
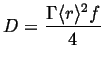 |
(13-27) |
and in general for a point source in ![]() dimensions:
dimensions:
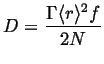 |
(13-28) |
![]()
![]()
![]()
Next: About this document
...