Solution Strategies
A number of different methods of finding a closed-form solution of the diffusion equation have been briefly described. Each one has a particular type of domain, boundary condition, or initial condition to which it is particularly suited.
However, many problems will not fall into these categories--and even if they do the solution may be either too difficult or impossible to obtain. It may be said with some confidence that most problems that you as professional materials scientists will face may be described thus.
The following five step program is designed to aid you in your quest.1
Brute Force: Numerical Methods
A closed-form solution is always preferable. From a closed-form solution, one can distinguish important physical parameters from less important ones; one can analyze limiting cases and deconstruct a solution to visualize its physical implications. However, closed-form solutions are sometimes time-consuming or impossible.
Numerical methods can be useful as a last (brute force) resort. Furthermore, numerical methods can also be a useful part of finding a closed-form solution--the visualization of a numerical solution will often provide clues of useful approximations or solution strategies.
At any rate, the tools and techniques of numerical methods have become part of the requisite apparatus of a materials scientist. A few methods of numerically solving the diffusion equation are introduced below. These are not necessarily the best methods--or the fastest (which can be an entirely different thing altogether). However, they are sufficiently general as to serve as a starting point for many numerical methods.2
A typical first approach is to discretize space so that
the solution at any one time can be represented by
values at a set of points
![]() and the
values that may be interpolated between them.
and the
values that may be interpolated between them.
In the finite difference approach, the values on the grid can be used and a discrete version of a spatial derivative is obtained in terms of differences at the grid points.
For instance, in two dimensions, a discrete version of
the Laplacian on a square grid of size ![]() ,
,
![]() , may derived directly
from the definition of a derivative:
, may derived directly
from the definition of a derivative:
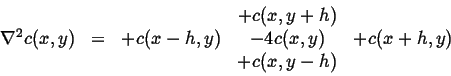 |
(09-1) |
In the finite element approach, a fitting function such as a polynomial is obtained for the regions between the points and the coefficients of the fitting function are determined by the values at specified points (nodes).
In each case, the spatial derivative can be used to iterate the solution in time.
In the forward differencing method, the definition
of the time derivative is used to infer the solution
at some time
![]() later, e.g. for the diffusion
equation:
later, e.g. for the diffusion
equation:
| (09-2) |
Another method, called the Implicit or Crank-Nicholson method, uses part of the previous solution and part of an implicit future solution to extend the stability condition. This increases the numerical stability at the expense of having to invert a set of linear equations to obtain the `future' solution.
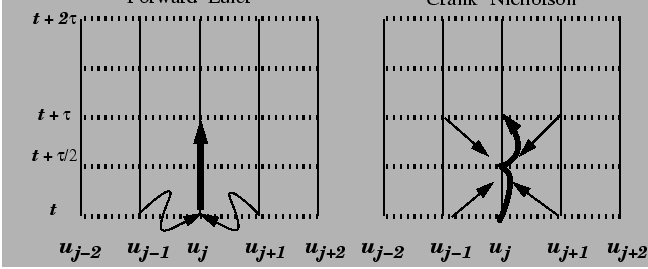 |
Another method is called the spectral method and is very powerful for solving the diffusion equation. They work somewhat in the same way that the Laplace transform method works--a derivative is transformed into an algebraic operation.
In particular, the Fourier spectral method is commonly used because of the existence of very fast techniques to perform the transformation operations (i.e., Fast Fourier Transforms--FFTs).
In a nutshell, the Fourier spectral method is implemented by representing the spatial part of the field as a series of trigonometric functions:
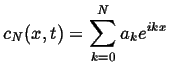 |
(09-3) |
The diffusion equation can be written as ![]() independent ordinary
differential equations (one for each coefficient of each wavelength):
independent ordinary
differential equations (one for each coefficient of each wavelength):
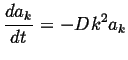 |
(09-4) |
Each of the ![]() ODEs is stable (increasingly more stable with large
ODEs is stable (increasingly more stable with large ![]() or short wavelengths).
A finite difference approach can be applied to each of the coefficients:
or short wavelengths).
A finite difference approach can be applied to each of the coefficients:
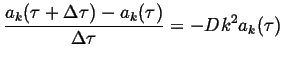 |
(09-5) |
So, the prediction of the future value of each coefficient can be solved simply and implicitly:
| (09-6) |
The real space time-dependent solution can be obtained by application of an FFT.
More details may be found in the textbook and its cited references.
Diffusion as a Molecular Process
The derivation of the diffusion equation followed from consideration of a continuum distribution of conserved particles. A treatment of individual molecular or atomic motions as part of a statistical ensemble of diffusing particles will prove to be not only consistent with the continuum approach, but will provide new physical concepts that enhance understanding of diffusive processes.
Below, the fundamental diffusive process--an atomic or molecular
displacement--is treated as a random jump occurring with
an average frequency ![]() .
It is instructive to consider how this simple model of random atomic
jumps corresponds to the various diffusion systems, or diffusivities
discussed above.
.
It is instructive to consider how this simple model of random atomic
jumps corresponds to the various diffusion systems, or diffusivities
discussed above.
First of all, if a jump is truly random, then the probability of
a given jump giving a net displacement
![]() must
be exactly the same as jump with displacement
must
be exactly the same as jump with displacement
![]() .
Therefore, the expected displacement,
.
Therefore, the expected displacement,
![]() ,
of a particle after one or more jumps must be identically zero.
Furthermore, the expected velocity of the particle,
,
of a particle after one or more jumps must be identically zero.
Furthermore, the expected velocity of the particle,
![]() ,
must also be zero.
Considering the Einstein drift equation
,
must also be zero.
Considering the Einstein drift equation
![]() ,
it must be concluded that the random walk treatment corresponds to
the physical experiment that
,
it must be concluded that the random walk treatment corresponds to
the physical experiment that
![]() , which is precisely
the case that is intended for the measurement of the self-diffusivity
, which is precisely
the case that is intended for the measurement of the self-diffusivity ![]() ;
i.e.
a diffusion couple of two alloys of the same composition, but differing in
isotopic concentration.
;
i.e.
a diffusion couple of two alloys of the same composition, but differing in
isotopic concentration.
Secondly, if the jumps are assumed to take place on a crystalline lattice,
then each random displacement ![]() will be selected from a small
subset of all the possible displacements that would be available in the
more general case of diffusion in a gas.
Treating the general case first, as is done below, leaves the diffusion on
the lattice as particular case.
will be selected from a small
subset of all the possible displacements that would be available in the
more general case of diffusion in a gas.
Treating the general case first, as is done below, leaves the diffusion on
the lattice as particular case.
Third, for a process to be completely random, there can be no restriction on the availability of a nearby empty site--the probability of an empty site cannot appear in the simple model of random walk. In the simple random walk process, two atoms may occupy the same space. Therefore, the simple random walk treatment should not correspond to substitutional diffusion on a crystal lattice. However, substitutional crystalline diffusion can be treated as a sequence of random hops on a lattice if the ``particle'' that hops is one of a infinitely dilute concentration of vacancies-a vacancy will always have an occupied neighboring site to hop into in the dilute limit.
In the treatment of the random walk, the average rate at which a walker (i.e. an atom or molecule) takes steps is an empirical frequency
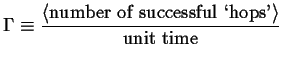 |
(09-7) |
Diffusion as a Random Walk Process
Let ![]() be the average rate that a random walker (an atom or molecule)
`take steps.'
be the average rate that a random walker (an atom or molecule)
`take steps.'
![]() is an average frequency.
is an average frequency.
![]() be the position of a
particular random walker:
be the position of a
particular random walker:
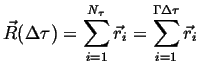 |
(09-8) |
What is meant by a ``random jump'' is not specified, but could be represented by a number of different processes:
In either case, the expected value
![]() ;
this is an indication that no particular direction is favored and
that the driving force
;
this is an indication that no particular direction is favored and
that the driving force
![]() for a random walk.
for a random walk.
However, it should be intuitively clear that the distance
between two particles should increase with time.
This distance is measured by the spread, or second moment, of the
distribution
![]() :
:
This can be rewritten as a sum along the diagonal and off-diagonal terms:
Using the relationship
![]() ,
where
,
where
![]() is the angle between the
is the angle between the
![]() and
and
![]() jump-vectors.
Therefore,
jump-vectors.
Therefore,
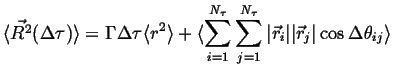 |
(09-12) |
If the lengths of the jumps do not correlate to the jump-angles:
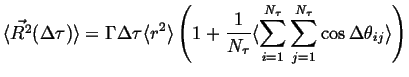 |
(09-13) |
Define the Correlation Factor, ![]() :
:
Therefore,
This is an important equation, it relates the spread of the
expected square displacements (or the second moment of the
probability distribution) per unit time with three factors
that are dictated by the mechanism of diffusion: the rate of
successful hops ![]() , the average square hop distance
, the average square hop distance
![]() ,
and a factor related to the correlation between hops,
,
and a factor related to the correlation between hops, ![]() . If every
hop is uncorrelated and the probability of positive displacement
. If every
hop is uncorrelated and the probability of positive displacement ![]() is exactly balanced by an equal probability
is exactly balanced by an equal probability ![]() then
then ![]() .
.
Diffusion as a Time-Dependent Probability Distribution
In the last section, the expected position and the
expected square displacement of a particle was calculated
by considering the statistics of a sequence of random jumps.
The concept of statistics can be coupled with that of
a probability distribution.
The probability of finding a particle after a time
![]() will
be determined and will be related to the form of a point source
solution of the diffusion equation.
will
be determined and will be related to the form of a point source
solution of the diffusion equation.
Consider a sequence of ![]() random jumps on a one-dimensional
lattice.
If the random walker is at position
random jumps on a one-dimensional
lattice.
If the random walker is at position ![]() after
after ![]() jumps (after starting at
jumps (after starting at ![]() ), then the number of jumps
to the right
), then the number of jumps
to the right ![]() and to the left
and to the left ![]() must satisfy:
must satisfy:
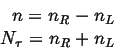 |
(09-16) |
The number of different ways that a random jumper could land
at site ![]() from the origin is given by the
binomial coefficient:
from the origin is given by the
binomial coefficient:
Therefore the probability of getting to site ![]() after
after ![]() jumps is:
jumps is:
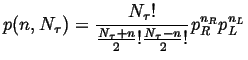 |
(09-18) |
If the probability of jumping right ![]() the probability
of jumping left, then
the probability
of jumping left, then
| (09-20) |
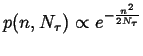 |
(09-21) |
Using
![]() and
and
![]() :
:
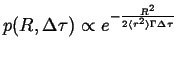 |
(09-22) |
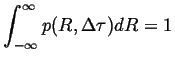 |
(09-23) |
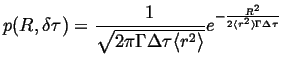 |
(09-24) |
Comparing this with the fundamental point solution in 1D:
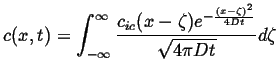 |
(09-25) |
The probability distribution can be used to identify the diffusivity with a random process:
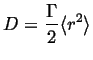 |
(09-26) |
Relation of the Self-Diffusivity to a Random Walk
The notion of the continuum limit for the concentration,
![]() of
particles is consistent with an interpretation of the concentration related
to a probability of finding a particle of a given type within a small
distance of the point
of
particles is consistent with an interpretation of the concentration related
to a probability of finding a particle of a given type within a small
distance of the point ![]() at a time
at a time ![]() .
Treating the concentration as a probability distribution, the second
moment of the distribution is related to the mean-square displacement
from the average displacement:
.
Treating the concentration as a probability distribution, the second
moment of the distribution is related to the mean-square displacement
from the average displacement:
Suppose all of the particles are located at the origin at
time ![]() , then if diffusion takes place in three dimensions:
, then if diffusion takes place in three dimensions:
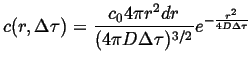 |
(09-28) |
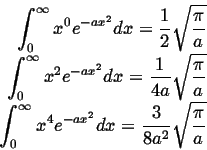 |
(09-29) |
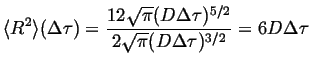 |
(09-30) |
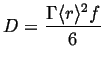 |
(09-31) |
Using the point source in two dimensions, the analogous result for diffusion in one dimension is:
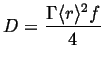 |
(09-32) |
and in general for a point source in ![]() dimensions:
dimensions:
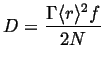 |
(09-33) |