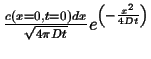
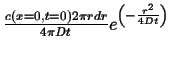
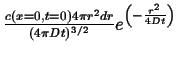
Fundamental Solutions with Different Dimensionalities
A solution for a point source initial condition with diffusion in one dimension was derived in the last lecture. The same solution would naturally apply to a line source diffusing into a plane or for a plane source diffusion into three-dimensional space.
The same method can be used to find fundamental solutions for cases where the finite source is a object of a given dimensionality embedded in an infinite space of larger dimension. This is called the ``co-dimension'' and it is the dimensionality of the infinite region minus the dimensionality of the embedded object.
All the pertinent examples are contained in the following table:
| Co-dimension | Example | Symmetric Part of |
Fundamental Solution |
| Point on Line | |||
| 1 | Line on Plane |
|
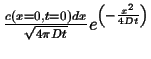 |
| Plane in 3D | |||
| 2 | Point in Plane |
|
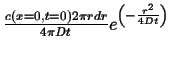 |
| Line in 3D | |||
| 3 | Point in 3D |
|
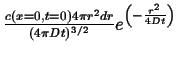 |
For example, the fundamental solution for co-dimension 2 can be used for arbitrary initial conditions for diffusion in an infinite thin film or the solution of co-dimension 3 can be used for initial conditions in three-dimensions.
However, each case above is strictly applicable to an infinite domain because that was an underlying assumption in the derivation of the point-source solution.
Method of Images or Symmetric Extension
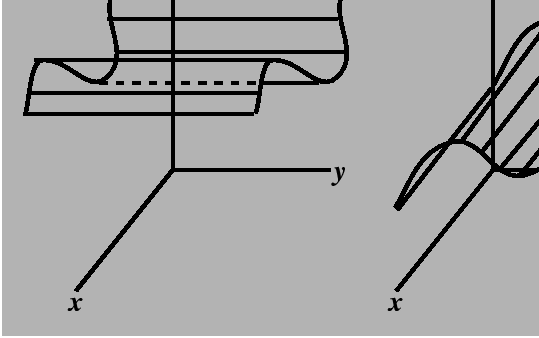
While the method of superposition of point-source solutions is generally always useful for infinite domains, it is possible to finesse the use of the fundamental solutions for other domains. The technique usually involves extending the computational domain by employing symmetries suggested by the boundary conditions.
A sufficiently complicated example serves to explain the use and generalization of the technique.
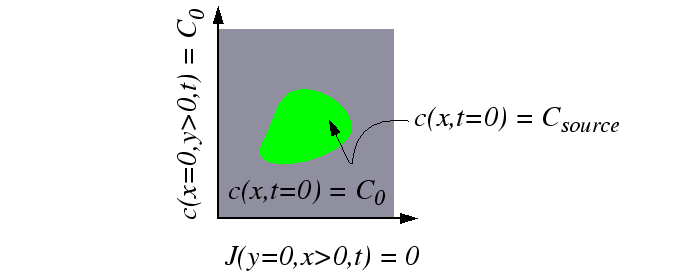 |
Consider the positive ![]() -axis.
The existence of an additional source term that is the image
from a mirror-reflection across the
-axis.
The existence of an additional source term that is the image
from a mirror-reflection across the ![]() -axis would satisfy the
no-flux condition along the
-axis would satisfy the
no-flux condition along the ![]() -axis.
This is due to the fact that each bit of the two source would contribute
in equal and opposite directions to the net flux at the boundary.
-axis.
This is due to the fact that each bit of the two source would contribute
in equal and opposite directions to the net flux at the boundary.
Next consider the positive ![]() -axis: if an sink term were present on the
negative
-axis: if an sink term were present on the
negative ![]() half plane so that every bit of diffusant would flow towards
the axis in the infinite problem would be removed by the sink, then
the concentration would not change.
It follows that if a ``negative source'' was present at the image
of the mirror reflected across the
half plane so that every bit of diffusant would flow towards
the axis in the infinite problem would be removed by the sink, then
the concentration would not change.
It follows that if a ``negative source'' was present at the image
of the mirror reflected across the ![]() -axis, then the fixed concentration
condition would be satisfied along the positive
-axis, then the fixed concentration
condition would be satisfied along the positive ![]() -axis.
-axis.
The method is illustrated in the figure below:
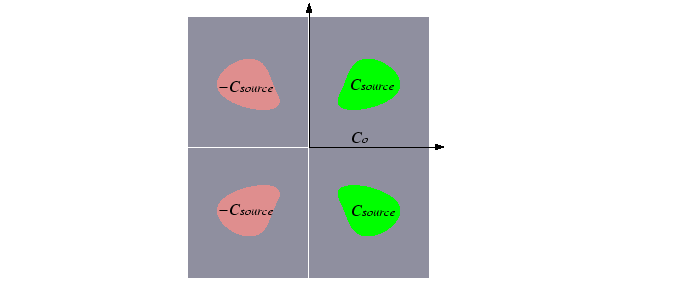 |
This method could be extended to a finite domain, but then one would need to sum over an infinite number of (periodic) images. Fortunately, there is a simpler method available for finite domains that has the infinite sums built in.
Periodic or Finite Domains: Separation of Variables
The Separation of Variables method is applicable for finite domains where the boundary conditions and initial conditions can be factored, i.e. separated by factors for each of the variables:
| (08-1) |
| (08-2) |
| (08-3) |
For the separation of variables, it is assumed that a factored solution exists, when (or if) it is found, uniqueness guarantees that it is the correct one for the specified initial and boundary conditions.
For example on the finite one-dimensional domain, ![]() ,
suppose for Dirichlet BCs:
,
suppose for Dirichlet BCs:
| (08-4) |
| (08-5) |
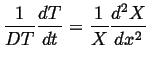 |
(08-6) |
Note that the left hand side depends only on ![]() and the right hand side depends
only on
and the right hand side depends
only on ![]() .
.
 |
A solution exists only if both sides equal the same constant. Let that
constant be ![]() .
.
Therefore, there are two ordinary differential equations to solve:
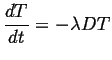 |
(08-8) |
The first ODE has well-known solutions:
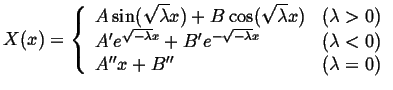 |
(08-9) |
| (08-10) |
If the concentration is to remain finite as
![]() , then
he only reasonable values for the separation constant for the given
BCs and ICs are
, then
he only reasonable values for the separation constant for the given
BCs and ICs are
![]() .
.
Applying the BCs to Eq. 8-7, ![]() , but there
are an infinite number of other values that will satisfy
the boundary conditions:
, but there
are an infinite number of other values that will satisfy
the boundary conditions:
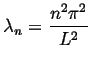 |
(08-11) |
The general solutions (for the BCs and ICs given above) are:
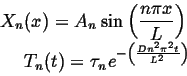 |
(08-12) |
However, to satisfy the initial conditions the general solution
must be taken as a linear superposition of each possible solution--and
with the weighting factor at ![]() chosen to satisfy the initial
conditions.
Therefore, seek
chosen to satisfy the initial
conditions.
Therefore, seek ![]() such that:
such that:
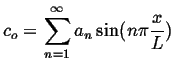 |
(08-13) |
Remarks on the Fourier Method of Solution
(A)
From the solution above, a periodic solution in
![]() can be constructed for
can be constructed for
![]() and
and
![]() for all integer
for all integer ![]() (use the
(use the ![]() in
in
![]() , etc).
, etc).
(B)
Note how each term in the Fourier series decays much faster than the previous term--the
rate at which amplitudes get smaller is exponential with smaller wavelengths.
This dependence on wavelengths is a useful intuitive device for understanding the diffusion equation.
 |
For example, consider two different initial conditions on the infinite domain
![]() :
:
The solutions ![]() and
and ![]() are obviously,
are obviously,
![\begin{displaymath}\begin{split}c_1 (x, t=0) = a \left[ 1 - \sin \left( \frac{2 ...
...\right) e^{-\frac{(4 \pi)^2 t}{D \lambda^2}}\right] \end{split}\end{displaymath}](img54.gif) |
(08-15) |
Time Dependent Boundary Conditions, Semi-Infinite Domains
The final analytic method for obtaining an analytic solution to to the diffusion equation is the method of Laplace transforms. This method is applicable to semi-infinite domains and is especially effective for problems with time-dependent boundary conditions.
The method of Laplace transforms is an example of operator calculus. In this case, the operator is a transformation of time derivatives to algebraic expressions in a transformation variable. The transformed diffusion equation becomes an inhomogeneous ordinary differential equation in the spatial variable. The ordinary differential equation is solved for the transformed boundary conditions and then the transformation is reversed--usually through a table of Laplace transform pairs.
The Laplace Transform is defined as the linear operator:
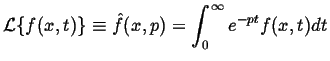 |
(08-16) |
The essential property of the Laplace transform is its operation on time derivatives:
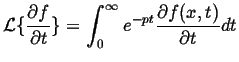 |
(08-17) |
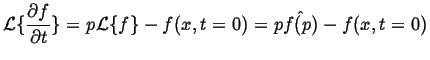 |
(08-18) |
The transform has no effect on spatial derivatives, therefore the transformed diffusion equation becomes:
Two Examples of the Laplace Transform Method
For this initial condition, the transformed diffusion equation, Eq. 8-19, becomes
For this problem, the homogeneous solution is:
| (08-21) |
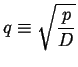 |
(08-22) |
The particular solution is:
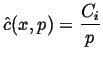 |
(08-23) |
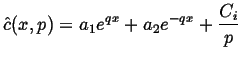 |
(08-24) |
The transformed boundary conditions become
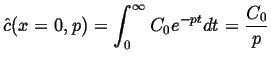 |
(08-25) |
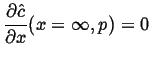 |
(08-26) |
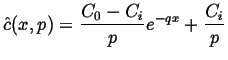 |
(08-27) |
This equation requires transformation back to the variable ![]() through
the inverse of a Laplace transform.
The inverses are usually much more difficult to find than the Laplace
transforms.
Fortunately, Laplace transforms and their inverses are usually tabulated
in math handbooks.
For example,
through
the inverse of a Laplace transform.
The inverses are usually much more difficult to find than the Laplace
transforms.
Fortunately, Laplace transforms and their inverses are usually tabulated
in math handbooks.
For example,
| Selected Laplace Transform Pairs | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
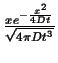 |
|
|
|
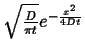 |
|
|
erfc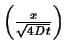 |
|
|
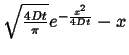 erfc erfc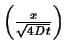 |
So, the solution can be obtained through the use of the above table:
![$\displaystyle c(x,t) = (C_0 - C_i) \left[ 1 - \ensuremath{\mbox{erf}}\left( \ensuremath{\frac{x}{\sqrt{4 D t}}}\right) \right] + C_i$](img97.gif) |
(08-28) |
For a second example with time-dependent solutions,
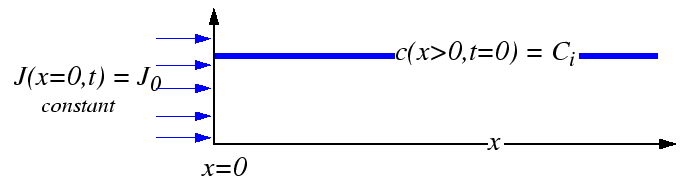 |
For this case, the transformed diffusion equation is the same as that calculated in the previous example:
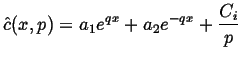 |
(08-29) |
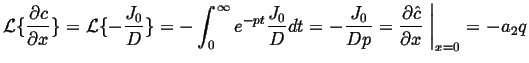 |
(08-30) |
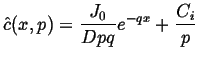 |
(08-31) |
![$\displaystyle c(x,t) = C_i + \frac{J_0}{D} \left[ \sqrt{\frac{4Dt}{\pi}} e^{\frac{-x^2}{4Dt}} - x \; \mbox{\em {erfc}}(\frac{x}{\sqrt{4Dt}})\right]$](img102.gif) |
(08-32) |
Therefore, the surface concentration changes as ![]() :
:
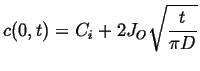 |
(08-33) |
Anisotropic Diffusion Coefficients
The methods of solution that have been treated do not account for the general case of an anisotropic diffusion coefficient. However, a simple strategem can be used to reconstruct the diffusion equation from its tensor form into the scalar form that is treated above.
Recall form of the the flux relationship in a particular frame of reference:
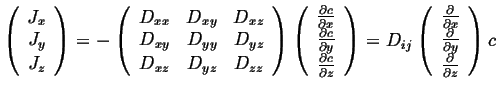 |
(08-34) |
The diffusion equation becomes:
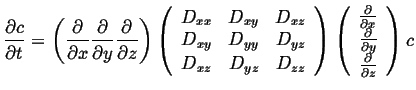 |
(08-35) |
First, find the rotation ![]() which diagonalizes
which diagonalizes
![]() :
:
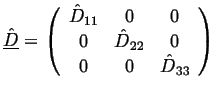 |
(08-36) |
The
![]() are the eigenvalues of
are the eigenvalues of
![]() and the coordinate
frame of reference of
and the coordinate
frame of reference of
![]() have axes parallel to the
eigenvalues of
have axes parallel to the
eigenvalues of
![]() .
.
The diffusion equation is much simpler in the eigenframe:
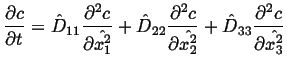 |
(08-37) |
Define an effective diffusivity ![]() :
:
| (08-38) |
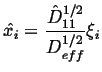 |
(08-39) |
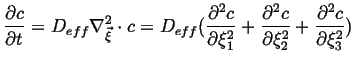 |
(08-40) |