Scaling and the Diffusion Equation
Note that the diffusivity has units (number
![]() cm
cm![]() )/s;
therefore,
)/s;
therefore, ![]() is dimensionless.
is dimensionless.
Introduce a dimensionless variable ![]() :
:
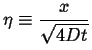 |
(07-1) |
Suppose for a particular problem, that the boundary and
initial conditions are also invariant to this scaling
implied by ![]() , in other words, if the length scale is tripled (yards
instead of feet) then the time scale for the boundary conditions is
multiplied by a factor of nine.
Or, under the scaling,
, in other words, if the length scale is tripled (yards
instead of feet) then the time scale for the boundary conditions is
multiplied by a factor of nine.
Or, under the scaling,
| (07-2) |
An example of such a problem would be the ``step-function'' initial conditions
with either Dirichlet or zero-flux Neumann boundary conditions at
![]() :
:
Initial conditions:
| (07-4) |
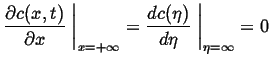 |
(07-5) |
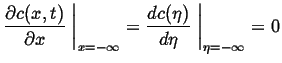 |
(07-6) |
Using the definition for ![]() :
:
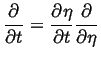 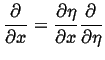 |
(07-7) |
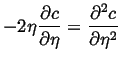 |
(07-8) |
Let
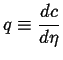 |
(07-9) |
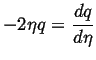 |
(07-10) |
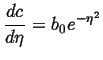 |
(07-11) |
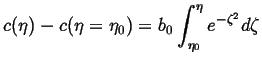 |
(07-12) |
Let
![]() and with the step-function initial conditions,
and with the step-function initial conditions,
![]() ,
,
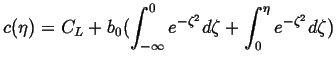 |
(07-13) |
or, by introducing another constant for ![]() ,
,
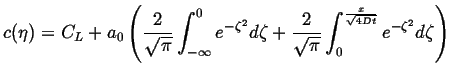 |
(07-14) |
The integral with an argument is just some function with a peculiar name:
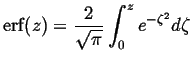 |
(07-15) |
So, the solution to the one-dimensional step function IC uniform diffusion equation is:
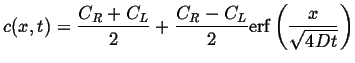 |
(07-16) |
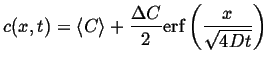 |
(07-17) |
Short Distances, Long Times
An additional and useful property of the error function is that
![]() for
for ![]()
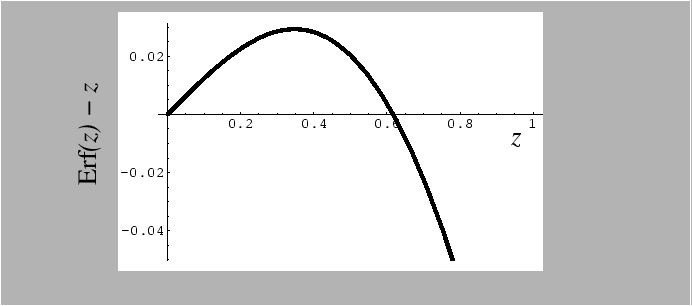 |
Because the scaling parameter
![]() is small for
long times
is small for
long times
![]() where
where ![]() is the characteristic
diffusion time:1
is the characteristic
diffusion time:1
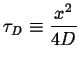 |
(07-18) |
| (07-19) |
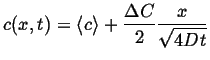 |
(07-20) |
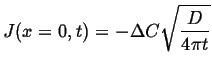 |
(07-21) |
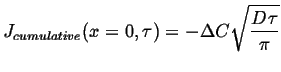 |
(07-22) |
Superposition Example
The simple solution that was developed above can be used with the method of superposition to develop a large number of solutions.
For example, suppose the initial conditions are changed so that
there is a finite source of material diffusing into an infinite
material and the finite source is confined to slab of with
![]() in the
in the ![]() -direction but extending infinitely in
the
-direction but extending infinitely in
the ![]() - and
- and ![]() -directions.2
-directions.2
These initial conditions can be obtained by summing two known solutions, i.e. those for the initial conditions:
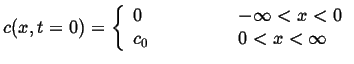 |
(07-23) |
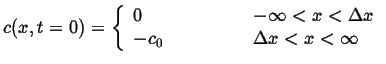 |
(07-24) |
The solution is just the sum:
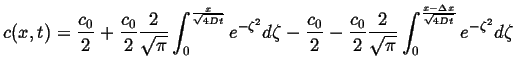 |
(07-25) |
It will be beneficial to reflect on what kinds of problems (i.e. which
initial and boundary conditions) will admit solutions from scaling
and then subsequent summing of solutions.
First for the scaling solution, the boundary and initial conditions
had to be invariant under the scale factor
![]() --this
is usually the case for infinite domains with zero flux conditions
at
--this
is usually the case for infinite domains with zero flux conditions
at
![]() .
Second, the summing method works when each solution that is to
be summed also satisfies scaling--therefore the initial
conditions for the particular problem must also be invariant.
Typically, these methods are useful in the infinite domain.
.
Second, the summing method works when each solution that is to
be summed also satisfies scaling--therefore the initial
conditions for the particular problem must also be invariant.
Typically, these methods are useful in the infinite domain.
The One-Dimensional Fundamental Solution
The solution for ``point-source'' initial conditions will prove to
be quite useful for cases when the addition of a large number of
solutions generate the initial conditions for a particular
problem.
The solution obtained in Eq. 7-26 can be used
to obtain the fundamental solution.
Expanding in powers of small
![]() :3
:3
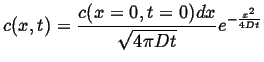 |
(07-27) |
Many other solutions by summing point source solutions,
In general,4for almost any initial conditions
![]() on the 1D infinite domain with zero
flux at
on the 1D infinite domain with zero
flux at
![]() ,
,
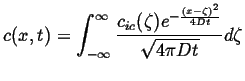 |
(07-28) |
Other Fundamental Solutions
The same method can be used to find fundamental solutions for cases where the finite source is a object of a given dimensionality embedded in an infinite space of larger dimension. This is called the ``co-dimension'' and it is the dimensionality of the infinite region minus the dimensionality of the embedded object.
All the pertinent examples are contained in the following table:
| Co-dimension | Example | Symmetric Part of |
Fundamental Solution |
| Point on Line | |||
| 1 | Line on Plane |
|
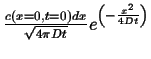 |
| Plane in 3D | |||
| 2 | Point in Plane |
|
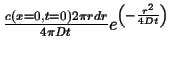 |
| Line in 3D | |||
| 3 | Point in 3D |
|
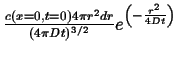 |