 |
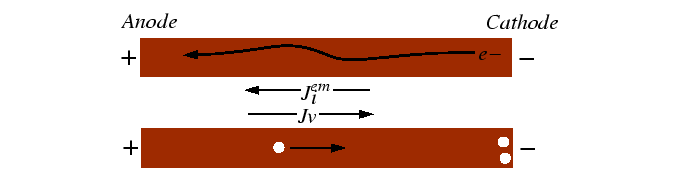
Electromigration
Electromigration is a kinetic effect that has consequences for the reliability of narrow conductors. In electromigration, there is a contribution to the net flux of atoms due to a potential difference across a conductor.
 |
The same method of associating the various fluxes with a
single identifiable mechanism that was used in the analysis
of stress-assisted diffusion can be used in the case of
electromigration.
The generalized driving force will be shown to be the
gradient in electrochemical potential,
![]() ,
where
,
where ![]() is the magnitude of charge on the electron, and
is the magnitude of charge on the electron, and ![]() is the number of charges on the diffusing ionic species.
is the number of charges on the diffusing ionic species.
Considering only motion of ions and counterflow of electrons, the generalized entropy production is:1
| (06-1) |
| (06-2) |
The generalized force-flux relationships are given by:
| (06-5) |
The interaction between the moving electrons and the host atoms is usually what one would intuitively expect--the atoms are dragged along with the charge carriers.
Anisotropy and Kinetic Coefficients
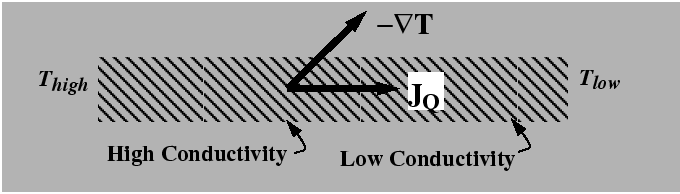
From consideration of expressions for the entropy production such a Eq. 6-3 and the hypothesis that the entropy production is always positive, it was reasoned that a flux would be antiparallel to its driving force. However, it is not necessary that the they are exactly antiparallel--only that there dot-product is negative. In anisotropic materials, the driving forces and fluxes are not generally in the same direction as illustrated in the following figure:
 |
A linear relationship between the forces and fluxes will now include all of the vector components:
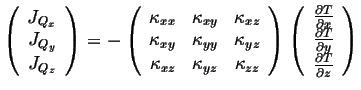 |
(06-6) |
or in component form:
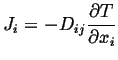 |
(06-7) |
| (06-8) |
From Onsager's hypotheses,
![]() and
and
![]() is positive definite.
is positive definite.
These material coefficients are examples of tensors. Neumann's principle implies that the symmetry of the tensor must include any symmetry elements of the point group of the symmetry of the underlying material. Note that Neumann's principle implies that the tensors must include--this doesn't note prevent them from having more symmetry than the underlying material and, in fact, may be isotropic.
Some examples of material tensor properties include the following:
| Tensor type | Linear Mapping Type | Tensor Type |
| example | example | example |
| material response | material property | applied field |
|---|---|---|
| vector (rank 1) | tensor (rank 2) | vector (rank 1) |
| current | electrical conductivity |
|
| vector (rank 1) | tensor (rank 3) | tensor (rank 2) |
| polarization | piezoelectric constant | stress |
| tensor (rank 2) | tensor (rank 4) | tensor (rank 2) |
| strain | compliance ( |
stress |
For example, the thermal conductivity of diamond is (in J/(msK)) approximately:
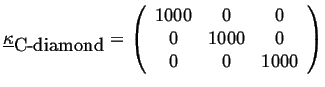 |
(06-9) |
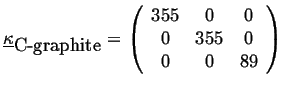 |
(06-10) |
Considering the possible anisotropy of material coefficients, the general force-flux relations will have tensors multiplying vector driving forces, e.g.
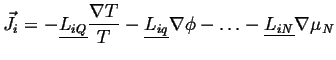 |
(06-11) |
or
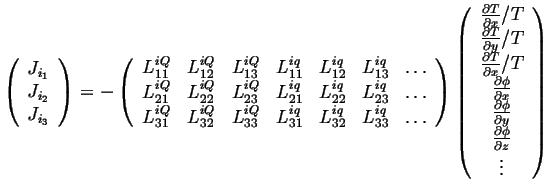 |
(06-12) |
In general
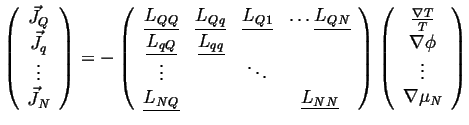 |
(06-13) |
The off-diagonal tensors are related through their transposes by Onsager symmetry. The diagonal matrices are symmetric and positive definite by positive entropy production.
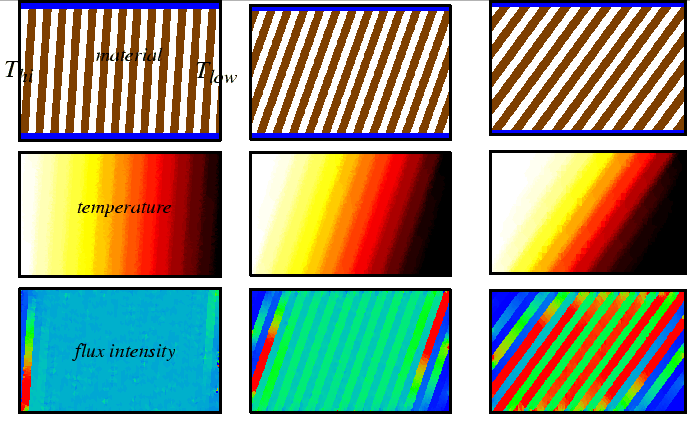 |
Flux, Divergence, and Accumulation Revisited: The Diffusion Equation
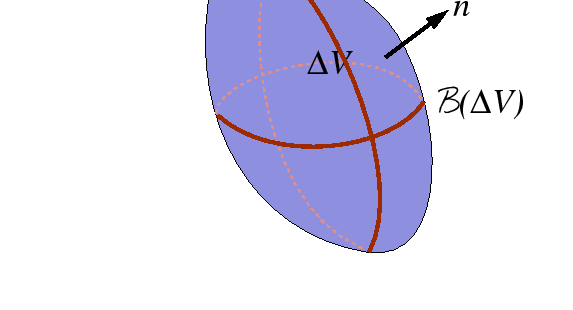 |
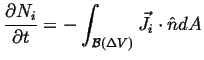 |
(06-14) |
Consider shrinking ![]() towards a given point.
Using the mean value theorem for integration,
towards a given point.
Using the mean value theorem for integration,
![]() can be replaced
with
can be replaced
with
![]() evaluated at some point
within
evaluated at some point
within ![]() .
Dividing both sides of Eq. 6-15 by
.
Dividing both sides of Eq. 6-15 by ![]() in this
limit:
in this
limit:
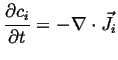 |
(06-16) |
Using the form of Fick's first law in the laboratory frame:
| (06-17) |
Combining the above equations, a single equation involving the concentration and its derivatives results:
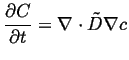 |
(06-18) |
A diffusion equation represents a local relation between how fast a quantity is changing and the divergence of its flux. Any quantity that is conserved will have a diffusion equation and can be derived with the same simple steps used above.
Most analytic solutions to the diffusion equation are for the
case of ![]() being both uniform and constant with
respect to composition.
As has been discussed previously, this is certainly not
the case for
being both uniform and constant with
respect to composition.
As has been discussed previously, this is certainly not
the case for ![]() .
However, it would be useful to have the wealth of useful
solutions that apply for constant
.
However, it would be useful to have the wealth of useful
solutions that apply for constant ![]() to apply to
materials problems of interest.3The solutions for constant
to apply to
materials problems of interest.3The solutions for constant ![]() are useful in limiting
case where the concentration does not vary wildly.
In this case, the value of
are useful in limiting
case where the concentration does not vary wildly.
In this case, the value of ![]() can be replaced
with levels of approximation to a constant concentration:
can be replaced
with levels of approximation to a constant concentration:
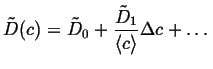 |
(06-19) |
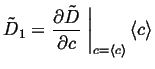 |
(06-20) |
The diffusion equation becomes:
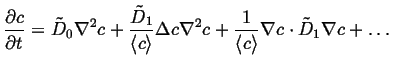 |
(06-21) |
The first solution in a method of successive approximations in
small ![]() and small
and small
![]() is simply,
is simply,
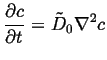 |
(06-22) |
The Diffusion Equation for Constant Diffusivity
The diffusion equation has a intuitively useful geometrical interpretation:
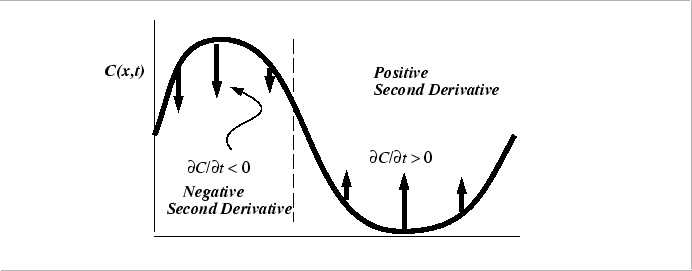 |
Generally, because there are two spatial derivatives equation and one time derivative in the diffusion equation, The specification of two spatial integration constants (the boundary conditions) and one time integration constant (the initial conditions) are required when stating a problem for solution..
Typically, boundary conditions (BCs) look like:
| (06-23) |
Initial conditions (ICs) are a function of space specified at a particular instant of time:
| (06-24) |
One very useful result of the diffusion equation being a
linear partial differential equation is superposition.
Suppose ![]() and
and ![]() are both solutions to the
diffusion equation, each with their own initial and boundary
conditions:
are both solutions to the
diffusion equation, each with their own initial and boundary
conditions:
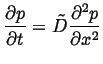 |
(06-25) |
| (06-26) |
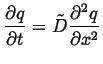 |
(06-27) |
| (06-28) |
| (06-29) |
Steady-State Solutions
Steady-state solutions generally apply at long times.4
The steady-state condition is that the solution ceases to be a function of time:
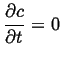 |
(06-30) |
So, to take a simple example of a one-dimensional problem on a finite domain, with uniform diffusivity and Dirichlet BCs:
Boundary conditions:
| (06-31) |
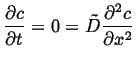 |
(06-32) |
Integrate once:
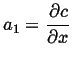 |
(06-33) |
| (06-34) |
Plug in the two
boundary conditions and solve for the two unknowns, ![]() and
and ![]() ,
to find the steady steady-state concentration profile:
,
to find the steady steady-state concentration profile:
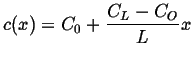 |
(06-35) |
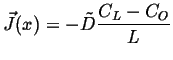 |
(06-36) |
For another simple example of a steady state solution, suppose the diffusivity is now a function of concentration, then the steady-state equation becomes:
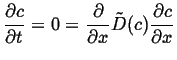 |
(06-37) |
Integrate once:
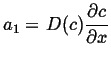 |
(06-38) |
Integrate again
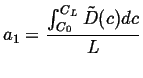 |
(06-39) |
which shows that
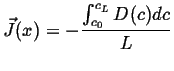 |
(06-40) |