| (05-1) |
Lattice Motion (Darken's Analysis)
Consider the effect of the net motion of vacancies on a lattice.
From the perspective of the lab frame, the lattice appears to move with the velocity ``marker atoms.''
Because,
| (05-1) |
The marker velocity must be related to the vacancy flux:
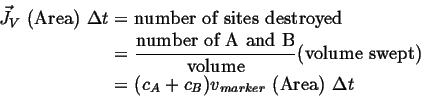 |
(05-3) |
Therefore
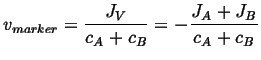 |
(05-4) |
Putting this into Eq. 5-2,
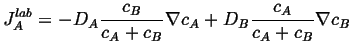 |
(05-5) |
If ![]() is small, and to good approximation
is small, and to good approximation
![]() :
:
| (05-6) |
which is Darken's equation and defines the interdiffusivity ![]() for diffusion
in an alloy.
for diffusion
in an alloy.
The Diffusivities
| Definitions and Relations for Diffusivities | |||
| Symbol | Name | Relation | Reference Frame |
| Interdiffusion Coefficient |
|
Laboratory | |
| Intrinsic Diffusivity |
|
Lattice | |
|
|
Laboratory | ||
|
|
|||
| Self-Diffusivity |
|
Either frame can be used | |
Motion of Marker Atoms
Last time, an equation for the average velocity of a inert ``marker'' atom was derived:
Kirkendall Effect
For a nice historical discussion of the Kirkendall effect,
see
http://www.tms.org/pubs/journals/JOM/9706/Nakajima-9706.html.
This weblet does a nice job of describing the intellectual resistance to the
current understanding that the motion of markers is
related to the differences (Zinc has an intrinsic diffusivity
about 2.5 times that of Copper at the temperature of
the Smigelskas-Kirkendall experiment, ![]() C)
in the intrinsic diffusion
coefficients during interdiffusion in an alloy.
C)
in the intrinsic diffusion
coefficients during interdiffusion in an alloy.
The mechanism behind the marker motion can be understood physically by the removal of lattice planes by vacancy absorption during dislocation climb on the side towards which the marker moves and the emission of vacancies by climb on the other.
However, the Kirkendall effect can also be explained with a very simple analogy to the interdiffusion of two gases with differing diffusivities. In fact, this phenomenon was known before the Kirkendall controversy.
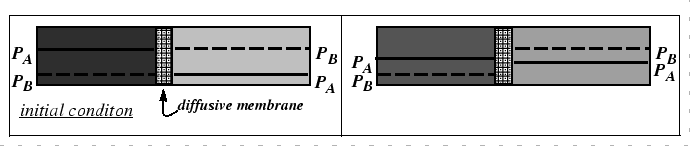 |
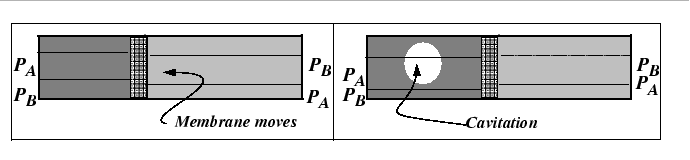 |
It is clear from the figures that, in a lattice, there will be contribution of stress to the driving force for diffusion.
Contribution of Stress to Diffusion
Consider the additional discussion of elastic terms are included into a thermodynamic framework that appears at the end of lecture 3. It was shown that:
| (05-9) |
If the entropy production in the absence of heat flow is considered:
Considering the combined effect of the motion of an interstitial, one can associate the various flux terms with a single diffusing species, i.e.,
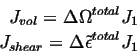 |
(05-11) |
The term inside the parenthesis becomes the generalized driving force for diffusion--it contains chemical plus elastic terms.
Often the deviatoric terms can be neglected, for instance for an interstitial in a cubic material, in this case (assuming ideal solution):
| (05-13) |
Addendum:
Stresses, Thermodynamics and Number of Independent Variables in
![]()
Sometime there is confusion associated with how to include stress
properly into the driving force.
the stress tensor
![]() .
This is not really part of kinetics but thermodynamics,
but a good question nonetheless.
.
This is not really part of kinetics but thermodynamics,
but a good question nonetheless.
Stress is a generalized way to think of pressure in materials that can support shears--a fluid is an example of a material that cannot sustain a shear at equilibrium. As a matter of fact, there is a nice proof in Gibbs that shows that the lowest energy state of a material is one that is in pure hydrostatic stress (pure pressure).
We have been writing the thermodynamic relation that relates the quasi-static changes in the entropy and the internal energy and the various ways the system can perform work as:
| (05-14) |
| (05-15) |
| (05-16) |
We are considering the appearance of the stress term in this question. Consider the term representing stress:
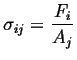 (i.e., (i.e., 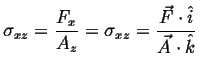 ) ) |
(05-17) |
![$\displaystyle \sigma_{ij} = \left[ \begin{array}{ccc} \sigma_{xx} & \sigma_{xy}...
...} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{array} \right]$](img51.gif) |
(05-18) |
It is a requirement of mechanical equilibrium that the
![]() tensor
is symmetric--it is also a guarantees that the quadratic form for
energy at equilibrium will have real eigenvalues, which is a little
like the Onsager symmetry hypothesis.
The symmetry reduces the number of components from 9 to 6.
tensor
is symmetric--it is also a guarantees that the quadratic form for
energy at equilibrium will have real eigenvalues, which is a little
like the Onsager symmetry hypothesis.
The symmetry reduces the number of components from 9 to 6.
There is one special and very simple case of elastic stress, and that is
called the hydrostatic stress.
It is the case of pure pressure and there are no shear (off-diagonal) stresses.
(i.e., all
![]() for
for ![]() , and
, and
![]() ).
An equilibrium system composed of a body in a fluid environment is always in hydrostatic stress:
).
An equilibrium system composed of a body in a fluid environment is always in hydrostatic stress:
![$\displaystyle \sigma_{ij} = \left[ \begin{array}{ccc} -P & 0 & 0 \\ 0 & -P & 0 \\ 0 & 0 & -P \end{array} \right]$](img55.gif) |
(05-19) |
If the body that is being stressed hydrostatically is isotropic, then its response is pure dilation (in other words, it expands or shrinks uniformly and without shear):
![$\displaystyle \epsilon_{ij} = \left[ \begin{array}{ccc} \Delta/3 & 0 & 0 \\ 0 & \Delta/3 & 0 \\ 0 & 0 & \Delta/3 \end{array} \right]$](img56.gif) |
(05-20) |
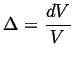 |
(05-21) |
So, for the case of hydrostatic stress, the work term has a particularly simple form:
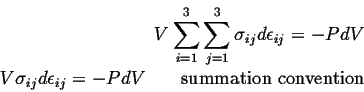 |
(05-22) |
This expression is the same as the energy density for a compressible fluid, such as an ideal gas.
Sometime, people like to include the ![]() terms in thermodynamics of solids because
it makes them feel comfortable.
The way to do this is do define the ``deviatoric stress:''
terms in thermodynamics of solids because
it makes them feel comfortable.
The way to do this is do define the ``deviatoric stress:''
![$\displaystyle \tilde{\sigma}_{ij} = \left[ \begin{array}{ccc} \sigma_{xx} - P &...
... \sigma_{yz} \\ \sigma_{xz} & \sigma_{yz} & \sigma_{zz} -P \end{array} \right]$](img59.gif) |
(05-23) |
| (05-24) |