| (04-1) |
One Independent Mobile Species: Highlights
The gradient in chemical potential is the only driving force and the motion of that species is the only flux:
| (04-1) |
The chemical potential can be related to local concentration through
the activity coefficient ![]() :
:
| (04-2) |
Therefore,
![]() can be related to
can be related to
![]() :
:
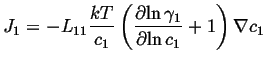 |
(04-3) |
If this is compared to the most simple version of Fick's first law,
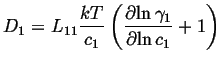 |
(04-4) |
The atomic mobility be defined by the the Einstien relation between the average drift velocity and the driving force,
| (04-5) |
The flux is related to the average velocity by:
| (04-6) |
Therefore
| (04-7) |
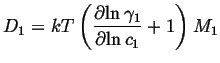 |
(04-8) |
If the solution is ideal--as in the case of mixture of
radioisotopes of an otherwise identical atomic species--then the
diffusivity is called the self-diffusivity ![]() and since
the activity coefficient is constant:
and since
the activity coefficient is constant:
| (04-9) |
Diffusion in a Crystal
When substitutional diffusion takes place inside a crystal, the number of sites is
conserved.
The site conservation provides an additional constraint.
The additional constraint, as will be shown below, leads to the consideration of
the chemical potential of the vacancy that is switching places with a diffusing
substitutional atom.
In other words, change in energy associated with a site after one diffusive
step has occured is
![]() --the chemical energy associated with
the site after the jump minus the chemical energy before the jump.
--the chemical energy associated with
the site after the jump minus the chemical energy before the jump.
Consider a system consisting of two mobile species ![]() and
and ![]() on a lattice
with
on a lattice
with ![]() vacancies:
vacancies:
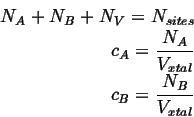 |
(04-10) |
The site fractions are given by
The volumes associated with each atom are
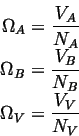 |
(04-12) |
Where
![]() which will be considered constant
and therefore:
which will be considered constant
and therefore:
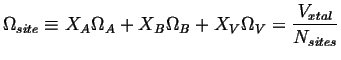 |
(04-13) |
The relation between the change in entropy per site with the internal energy and work terms when the only additional work term is the chemical work per site is:
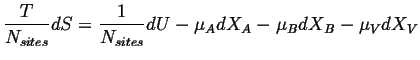 |
(04-14) |
or in terms of densities of extensive quantities:
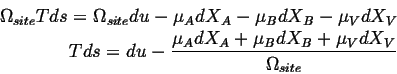 |
(04-15) |
Because the sites are conserved (Eq. 4-11),
![]() :
:
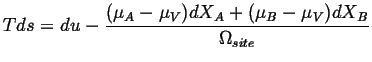
| (04-16) |
The expression for the entropy production is, for example including the heat flow term as well is:
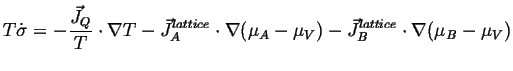 |
(04-17) |
Self Diffusion of an Isotope in a Crystal
The above analysis can be applied to isotopic diffusion which is traditionally used to obtain measurements of the self-difussion coefficient.
Let the isotope of ![]() be desginated by
be desginated by ![]() and while
and while ![]() and
and ![]() may
be assumed to be chemically identical, intrinsic mobilities may differ
due to their mass differences.
may
be assumed to be chemically identical, intrinsic mobilities may differ
due to their mass differences.
Writing out the linearized flux relationships for this case:
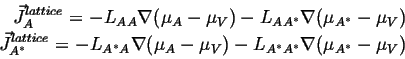 |
(04-18) |
If is can be assumed that the vacancies are everywhere in equilibrium,1then
![]() ; if, futhermore, the vacancy concentration gradient is constant (which
is consistent with the assumption of equilibrium), so that the concentration
gradients
; if, futhermore, the vacancy concentration gradient is constant (which
is consistent with the assumption of equilibrium), so that the concentration
gradients
![]()
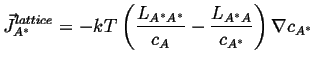 |
(04-19) |
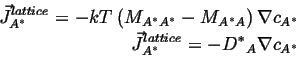 |
(04-20) |
If the solution is not ideal, then by direct extension, the intrinsic diffusivity is:
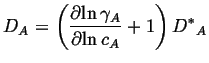 |
(04-21) |