Mathematical Background, cont'd
Fields
A field associates a physical quantity with a position,
![]() at a time,
at a time, ![]() .1A field may also be a function of time:
.1A field may also be a function of time:
![]() where
where ![]() is the physical quantity that
depends on location and time.
is the physical quantity that
depends on location and time.
Fluxes
Flux is an important vector field quantity in kinetics and it is important to understand it. It represents the rate at which ``stuff'' flows through a specified unit of area--an area is oriented in space.
Let
![]() be an oriented patch of area,
be an oriented patch of area,
![]() .
If
.
If ![]() is the rate at which
is the rate at which ![]() flows through
a unit area, it follows that
flows through
a unit area, it follows that
| (02-1) |
| (02-2) |
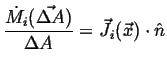 |
(02-3) |
Accumulation
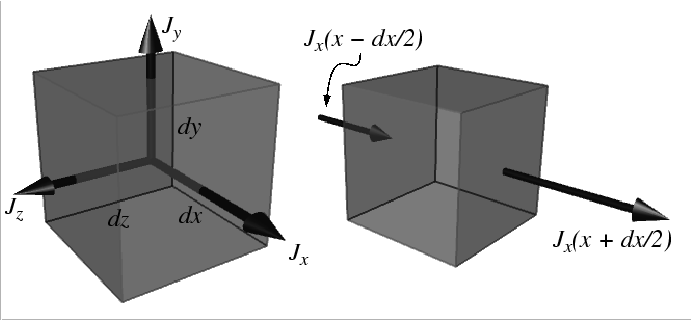 |
The rate at which ![]() accumulates in a volume
accumulates in a volume
![]() (with outward oriented normals)
during time interval
(with outward oriented normals)
during time interval ![]() is:
is:
| (02-4) |
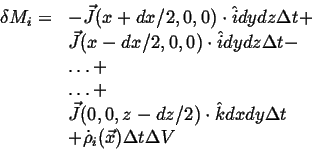 |
(02-5) |
Expanding to first order in
![]() , subtracting, and using the continuum limit,
, subtracting, and using the continuum limit,
The rate of accumulation of the density of an extensive quantity is minus the divergence of the flux of that quantity plus the rate of production
Note that Eq. 2-6 could have been derived directly from:
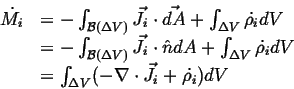 |
(02-7) |
Conserved and Unconserved Quantities
Conserved quantities are those that do not vanish from or spring into existence at any time or place. Therefore, the rate of production term in the accumulation must be identically equal to zero--for conserved quantities:
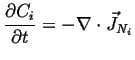 |
(02-8) |
Molecules are not conserved if chemical reactions take place.
Internal energy is conserved:
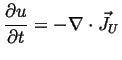 |
(02-9) |
Examples of things that are not conserved include magnetization or spin density, atomic order, and polarization. Entropy is not conserved, thus there must be an expression:
Introduction to Irreversible Thermodynamics
Equation 2-10 may seem sensible, but is it possible to form
a physical picture of what is meant by the flux of entropy
![]() ?
?
What is meant by the continuum limit of the entropy density, ![]() ?
?
One way to find a meaningful picture of the entropy density is to assume that equilibrium thermodynamics applies locally. Then, the expression for equilibrium changes,
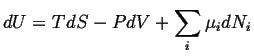 |
(02-11) |
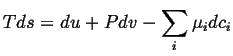 |
(02-12) |
To illustrate how the assumption of local equilibrium will be used, consider a closed system that does or receives no work from its surroundings--i.e. a system where entropy can only increase according to the second law.
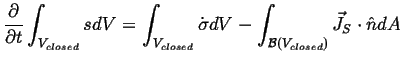 |
(02-14) |
where
![]() is the surface of the closed volume
is the surface of the closed volume
![]() and
and
![]() is the outward normal of that surface.
is the outward normal of that surface.
Supposing that the system does no
work, only heat contributes to
![]() at the surface:
at the surface:
The last term is (minus) the total heat that enters the system:
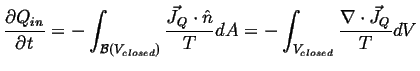 |
(02-16) |
If the surface is uniformly at constant temperature, then
This leads to a fundamental postulate of irreversible thermodynamics: ![]() or
or
Rewrite Eq. 2-18 using the assumption of local equilibrium
(2-13):
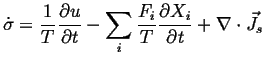 |
(02-19) |
To simplify writing, it is useful to introduce the ``summation convention'' where
any repeated index becomes an implied sum.
For instance,
the dot-product can be written as
![]() where in the final term the repeated index
where in the final term the repeated index ![]() is summed over all of its possible
values; for instance,
is summed over all of its possible
values; for instance,
![]() where
where
![]() are
the nine (3
are
the nine (3 ![]() 3) components of the stress tensor,
3) components of the stress tensor,
![]() are the nine
components of the strain
tensor,4
are the nine
components of the strain
tensor,4 ![]() is the electrostatic potential and
is the electrostatic potential and ![]() is charge density,
is charge density,
![]() and
and ![]() are the three (i.e.,
are the three (i.e., ![]() ) components of the applied and
induced magnetic fields, and
) components of the applied and
induced magnetic fields, and ![]() and
and ![]() are the
are the ![]() chemical potentials
and concentrations of the
chemical potentials
and concentrations of the ![]() independent chemical species.
independent chemical species.
Therefore, using the summation convention:
Using a version of the vector chain rule:
![]() :
:
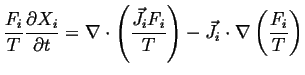 |
(02-21) |
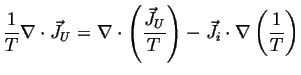 |
(02-22) |
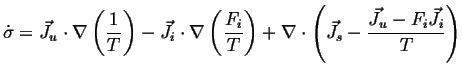 |
(02-23) |
Define:
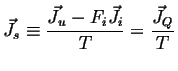 |
(02-24) |
Because ![]() is always positive, this implies a relation between the fluxes
and the gradients of the potentials:
Naively (but not necessarily),
is always positive, this implies a relation between the fluxes
and the gradients of the potentials:
Naively (but not necessarily),
![]() , must be antiparallel to
, must be antiparallel to ![]() ;
;
![]() , must be antiparallel to
, must be antiparallel to
![]() for the entropy
production to be everywhere positive.
for the entropy
production to be everywhere positive.
Consider quantity on the right-hand-side of Eq. 2-25 term-by-term:
| Conjugate Forces, Fluxes and Empirical Flux Laws for Unconstrained Components | ||||
| Quantity | Flux | Conjugate Force | Empirical Flux Law | |
| Heat |
|
Fourier's |
|
|
| Mass |
|
|
Modified5Fick's form |
|
| Charge |
|
|
Ohm's |
|