X-ray Diffraction
X-rays are electromagnetic radiation with wavelengths between about 0.02 A and 100 A (1A = 10-10 meters). The wavelength of X-rays is on an atomic level and is much smaller than that of visible light (3000 to 8000 A). Since X-rays have a smaller wavelength than visible light, they have higher energy and are more penetrative. Its ability to penetrate matter, however, is dependent on density of the matter. Therefore, X-rays are useful in exploring structures of atoms.
X-rays are produced in a device called an X-ray tube. The X-ray tube consists of an evacuated chamber with a tungsten filament at one end, called the cathode, and a metal target at the other end, called an anode. When electrical current is put through the filament, excited electrons from the tungsten are emitted. If a high potential difference is placed between the cathode (positive end) and the anode (the negative end), the emitted electrons move at high velocity from the filament to the anode target. The electron will strike atoms at the target, dislodging inner shell electrons of the target atom. As a result, electrons on the outer shell emit jump down to fill the void in the inner shell. Because the inner shells have lower energy than the outer shells, when an outer shell electrons jump to inner shells, they emit radiation in the form of high energy X-rays.
Because X-rays are bundles of separate waves, each wave can interact with on another either constructively or destructively. The interaction between waves is called interference. If waves are in phase meaning that each of their crests and troughs occur exactly at the same time, then the waves will stack together to produce a resultant wave that has a higher amplitude. This is called constructive interference. If they waves are out of phase, then destructive interference occurs and the amplitude of the resultant wave will be reduced. If waves are exactly out of phase by a multiple of n/(2*lambda) then there will be complete destructive interference and the resultant wave has no amplitude, meaning that it is completed destroyed.
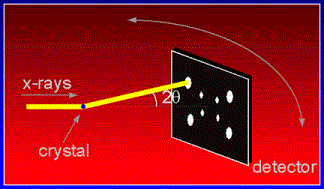
One of the best methods of determining a crystal's structure is by X-ray diffraction. In macromolecular x-ray diffraction experiments, an intense beam of X-ray strikes the crystal of study. In general, crystal diffracts the X-ray beam differently, depending on its structure and orientation. The diffracted X-ray is collected by an area detector. The diffraction pattern consists of reflections of different intensity which can be used to determine the structure of the crystal. However, many different orientations of the crystal need to be collected before the true structure of the crystal can be determined.
The resolution of an X-ray diffraction detector is determined by the Bragg equation:
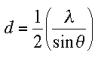
where d is the resolution of the detector, lambda is the incident x-ray wavelength, and theta is the angle of diffraction.
The setup of an X-ray detector is shown in the following:

The atoms in crystals interact with X-ray waves in such a way as to produce interference. Because crystal structures contain planes of atoms, each plane will reflect incident X-rays differently. For example, let two monochromatic X-ray beams (of a specific wavelength) strike a crystal structure at an incoming angle of theta. Ray 1 will reflect off of the top atomic plane while Ray 2 will reflect from the second atomic plane. However, because Ray 2 has to cross deeper into the atomic plane, it travels a distance 2a farther than Ray 1. If the distance 2a is equal to the integral number (n*lambda) of wavelength of two waves, then Ray 1 and 2 will be in phase, thus constructively interfere, when they both exit the crystal.
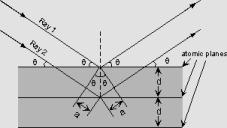
From Bragg's law, we know that n*lambda = 2d sin theta, therefore if we know the wavelength lambda of the X-rays going in to the crystal, and we can measure the angle theta of the diffracted X-rays coming out of the crystal, then we can determine the spacing between the atomic planes. This spacing is the called the d-spacing. If we now reorient the crystal to a different atomic plane, we can measure the d-spacing in other planes. By doing multiple x-ray diffractions at different crystal orientations, we can determined crystal structure and the size of the unit cell of the crystal.
Practically speaking, reorienting the crystal to every plane and measuring the diffraction angle theta to determine the d-spacing of each plane is very time consuming. Thus, the powder method is often used to speak up the process. In this method, the crystal of study is ground into fine powder. The find powder contain small granules of crystals with random orientations. If we have enough powder randomly oriented on the surface, we expect some of the different atomic planes to lie parallel to the surface. Therefore, if we scatter an incident X-ray beam from 0 to 90 degrees, we should find all the angles where diffraction occurred. Each of these angles will correspond to a different atomic spacing. The instrument used to make these measurements is the X-ray powder diffractometer. To rotate both the X-ray tube and the detector through the 90 degrees angle, a goniometer is used.
