Fourier Transforms in Crystallography
Because we have different waves of X-rays superimposed on one another during diffraction, it is difficult to isolate the contribution of each diffraction event to determine the lattice structure. Therefore a mathematical tool known as the Fourier transform is used. A Fourier transform is a representation of some function in terms of a set of sine-waves. The set of sine-waves of different frequencies has orthogonal properties. In general, any function can be represented in terms of a Fourier series, which is just the sum of enough sine-waves of the appropriate frequency, amplitude and phase. If we have a function that contains superpositions of many different waves with different amplitudes, freqency and phase, such as in our case of the diffracted x-ray signal we pick up on our detector, we can perform an inverse Fourier transform to determine the individual frequencies of the diffracted X-ray waves as well as their relative strengths.
Example of FT and Superposition
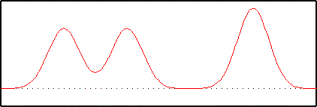
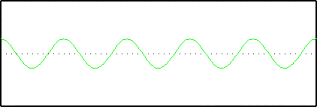
To illustrate the notion of stacking sine-waves, consider an imaginary one-dimensional crystal. The unit cell contains three atoms: two carbons and an oxygen. From our X-ray diffraction experiment, we determined that the electron density in the unit cell looks like the following:
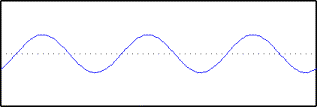
Our first step is to try to represent this electron function in terms of sine-waves. The first sine wave has a frequency of 2, meaning that the wave repeats twice over the unit cell. One of the peaks correspond to the oxygen, and the other the two carbons as shown here:
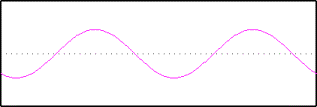
The second sine wave has a frequency of 3, meaning that there are three repeats of the wave across the unit cell. It has a different phase, in other words we start at a different place on the wave. The amplitude is also different as shown here:
Lastly, we add the last sin wave with a frequency of 5. You see that two of the peaks of this wave are lined up with the carbon atoms:
When we add all three waves together, we will get back our original wave as shown below.
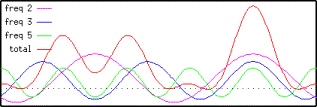
In this fashion we have just shown that we can decompose our original density function into three different sine-waves. Since different lattice spacings will diffract X-rays differently, each decomposed sine-wave will give us a characteristic of the crystal structure. Therefore by reconstructing the frequency spectrum from the inverse Fourier transform, we can determine the relative strength of different waves that are contributing to form our signal. Therefore, performing an inverse Fourier transforms on the signal will give us valuable information on our crystal structure.
In our example, you can see that the sum of the three sine-waves is a good approximation of the original density function. This indicates that we can describe the unit cell quite well using only three sine-waves, given the correct choice of frequency, amplitude and phase. In general however, we would need to use many different sine-waves to build an accurate reconstruction of our original function
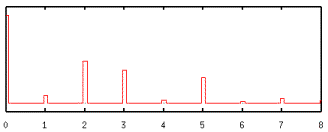
Now if we look at the inverse Fourier transform of the unit cell, we find that the result consists of a series of peaks, the largest of which are at 2, 3 and 5 on the frequency access. These peaks correspond exactly to the sine-wave frequencies that we used to reconstruct the unit cell. The height of the peaks also correspond to the amplitude of the three waves: