
what is the energy (voltage) of a unit positive charge located at (x,y,z)
Multidimensional Integral over Irregular Domains
We will attempt to model the energy of ion just above one half of a triangular capacitor. Suppose there is a uniformly charged surface (σ≡charge/area=1) occupying an equilaterial triangle in the z=0 plane:

what is the energy (voltage) of a unit positive charge located at (x,y,z)
The electrical potential goes like ![]() , therefore the potential of a unit charge located at (x,y,z) from a small surface patch at (ξ,η,0) is
, therefore the potential of a unit charge located at (x,y,z) from a small surface patch at (ξ,η,0) is  =
= 
Therefore it remains to integrate this function over the domain η∈(0,![]() ) and ξ∈ (
) and ξ∈ (![]() ) , (
) , (![]() ))
)) 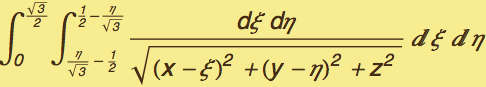
First we investigate how Mathematica deals with multiple integrals: It integrates over the last iterator first:

![]()
![]()
![]()
For example,consider the difference in the following two cases:
First, we integrate over x and y using the two iterators in Integrate with the order {y,0,1}, {x,0,y}. Tnen explicitely using two separate steps

![]()
![]()
![]()
Compared to
integrate over x and y using the two iterators in Integrate with the order {x,0,y},{y,0,1}. Tnen explicitely using two separate steps

![]()
![]()
![]()
| Created by Wolfram Mathematica 6.0 (24 September 2007) |