
Solving Systems of Equations
Consider the set of equations
x + 2y + z + t = a
-x + 4y - 2z = b
x + 3y + 4z + 5t = c
x + z + t = d
We illustrate how to use a matrix representation to write these out and solve them…
Start with the matrix of coefficients of the variables, mymatrix:


The system of equations will only have a unique solution if the determinant of mymatrix is nonzero.
![]()
![]()
![]()
![]()
The left-hand side of the first equation will be
![]()
![]()
and the left-hand side of all four equations will be
![]()
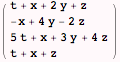
Now define an indexed variable linsys with four entries, each being one of the equations in the system of interest:
![]()
![]()
![]()
Solving the set of equations for the unknowns ![]()
![]()
![]()
| Created by Wolfram Mathematica 6.0 (06 September 2007) |