Solve problems in terms of the mass and natural frequency--eliminate the spring constant in equations by defining it in terms of the mass and natural frequency.
Resonance Phenomena by Solution of the ODE
The "periodic forcing function" can be any periodic function (i.e., a fourier series), but it is a bit simpler to analyze the effect of each mode separately. Below, the forcing function will be assumed to be ![]() cos(
cos(![]() t)
t)
Solve problems in terms of the mass and natural frequency--eliminate the spring constant in equations by defining it in terms of the mass and natural frequency.
![]()
![]()
Mathematica can solve the nonhomogeneous ODE with a forcing function at with an applied frequency:
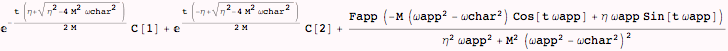
Consider the form of the above solution: The homogeneous part of the solution (i..e, the part that depends on constants C[1] and C[2]) depends only on the characteristic frequency, while the heterogeneous part includes the forcing and the characteristic frequency. From a first glance at the denominator in the heterogeneous term, it appears the amplitudes are maximized as ωapp → ωchar; and , it appears that, as long as the viscous term η is non-zero, the solution is bounded. However, this is not the case as will be shown below.
Consider the behavior of the general solution at time t=0. This will show that the homogeneous parts of the solution are needed to satisfy boundary conditions, even if the oscillator is initially at rest at zero displacement (i.e., y(0) = ![]()
![]()
![]()
Therefore, the C[1] and C[2] in the general solution, must pick up terms that depend on ωapp and these must be included in considerations of the limit ωapp → ωchar.
Consider the particular case of an oscillator at rest at zero displacement:
![]()

The resonant solution is the case: ωapp → ωchar
![]()

To analyze the resonant behavior when the viscosity η is small, the solution is expanded about small viscosity to second order:
(Below, the function Map is used with a pure function to simplify each of the terms resulting from a series expansion (n.b. Normal converts the series form into a normal form). Each term in the expansion is operated on in the following manner:
1) Convert any Exp[] into trignometric functions with ExpToTrig
2) Remove fractional powers of containing powers of real numbers with PowerExpand
3) Simplify
by using a pure function as the first argument to Map,
![]()

![]()


Of course, this leading behavior could have been obtained directly, viz
![]()
![]()
but, from the direct solution, one cannot obtain the behavior as the viscosity becomes small
Considering the appearance of the resonant solution, there may be another special case when η is near 2 M ωchar.
![]()
![]()
However, it appears that the only special feature is that, after very long times, the solution is a quarter-period out of phase.