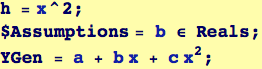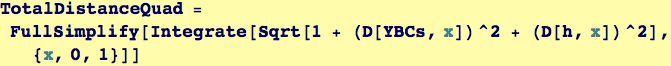Functionals: An Introduction to Variational Calculus by way of Variation of Parameters: Approximating the Geodesic
The introductory form of calculus of variations involves finding an unknown function, y = y(x), which maximizes or minimizes a specified definite integral of y(x).
As an introductory problem, we might as a question such as, "of all paths that traverse a rolling landscape, which one is the shortest?" The y(x) that minimizes the total length is called the geodesic.
The total length of a path over a fixed surface can be written as an integral of the unknown y(x) (this is worked out in the accompanying lecture notes)
L[y(x)] =  =
= 
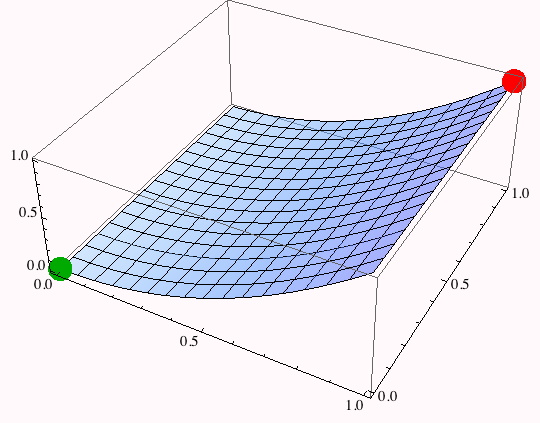
Suppose that the "hill" has the shape h(x) =  .
.
Here, the "real" problem of finding the geodesic from the infinite set of all paths connecting y(x=0) = 0 to y(x=1) = 1 will be replaced by looking at all second-order polynomials: y(x) = a + bx + c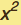 and then minimizing over the (constrained) parameters. This will be compared with the exact calculation which we will work out below via calculus of variations.
and then minimizing over the (constrained) parameters. This will be compared with the exact calculation which we will work out below via calculus of variations.
We specify a landscape and an arbitrary quadratic path (a function of three parameters)
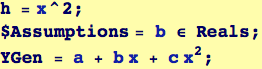
Illustrate this surface and identify the starting and ending points.

The general path must satisfy the boundary conditions:


There is one remaining free variable, it can be determined by minimizing the integral
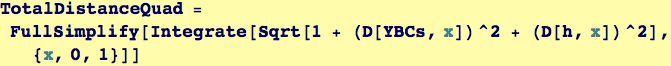

To get an idea of how the path' s distance compares with its shape, we can manipulate the path and display that path' s length
Interactive Path Modification and Length Calculation