
Visualizing Diffraction Patterns of Crystals Thermal Noise
Function to Create A Lattice of Squares :
NoisyLattice[TotalSize, LatticeVector1, LatticeVector2, SquareSize, RandomDisplacements]

First look at an example with no noise, we create a lattice of squares with lattice vectors (8,4) and (16,16). This function will create smaller unit cells if the last vectors are divisors of the total size. Here we set the edge of the square to 1 and indicate that we want 0,0 noise in the x,y directions.
![]()
![]()


We reconstruct the example from above, but introduce random unit displacements of the squares in the x and y directions.
![]()
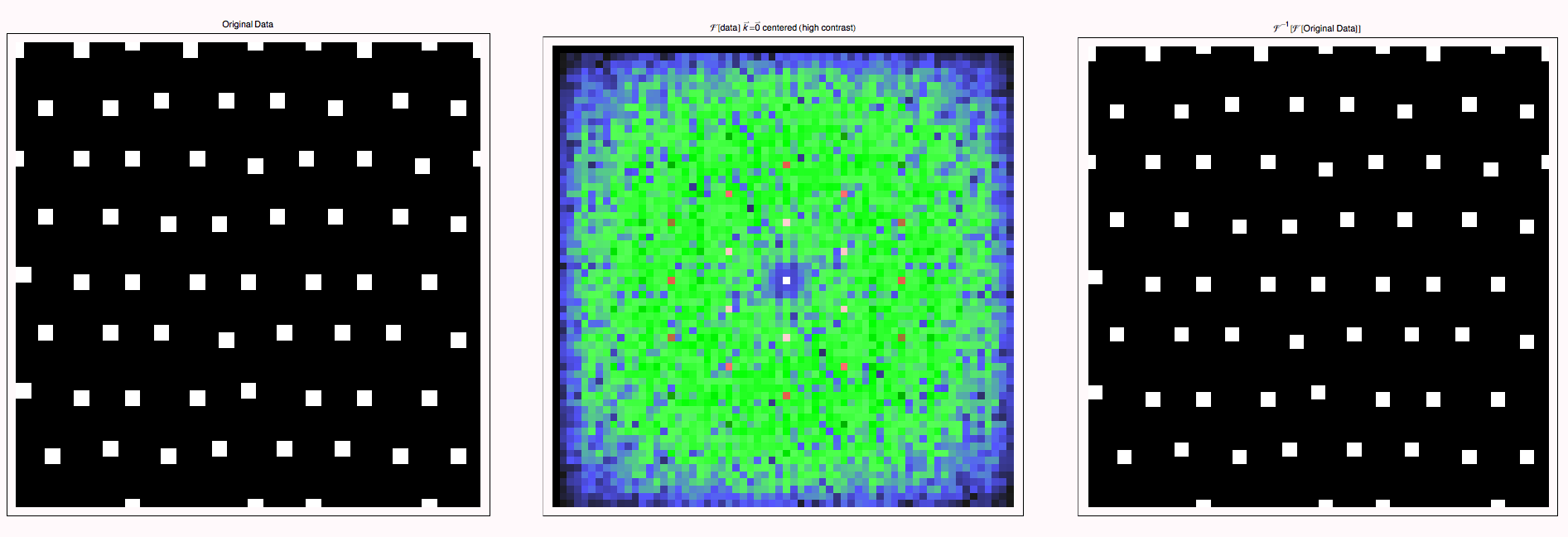

The appearance of diffuse intensity (e.g. the intensity that does not correspond to the bright spots for the ideal lattice) corresponds to random shifts in the original figure. This is a simulation of isotropic thermal vibrations. In crystals, the amplitudes would be larger in elastically soft directions. It is instructive to use the last two arguments in the NoisyLattice function to make the "noise" anisotropic and observe its effect on the diffration pattern--the streaks that you will observe correspond to observations in the TEM.
| Created by Wolfram Mathematica 6.0 (01 November 2007) |