Calculus of Variations: Euler Equation for the Geodesic
As derived in the notes, the condition for a curve to minimize an integral is given by the variational derivative, setting the variational derivative equal to zero produces the Euler equation
![]()
![]()
![]()
Calling VariationalD from the package "VariationalMethods"
![]()

Setting the variational derivative to zero is the Euler equation
![]()

The Euler equation is an ODE; this one has a closed-form solution.
![]()
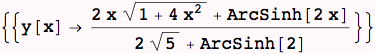
![]()

| Created by Wolfram Mathematica 6.0 (26 November 2007) |