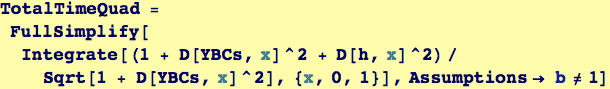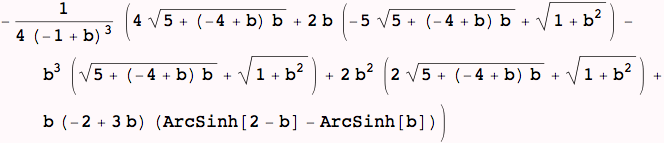Approximating the Brachiostone
The "quickest" path of running up-hill can be estimated with a model of how fast one runs up hill. Given a starting point y(x=0) = 0 and an ending point y(x=1) = 1, the question is to find, among all possible choices of path y(x) that connects the end and starting point, which is the one that takes the least time if there is a hill h(x) that has to be "run-up."
A reasonable model is that running speed is proportional to Cos(climbing-angle)--that is the velocity is 1 for running on a flat surface and goes to zero as the climbing-angle goes to 
Assuming that v(s) = Cos α(s) where α is the angle of incline (i.e., cos α=  /
/ then the time increment is
then the time increment is
derived from ds/dt= v(s): dt = ds/v(s), then
time=  = ∫
= ∫  = ∫
= ∫  dx
dx
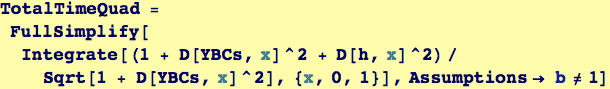
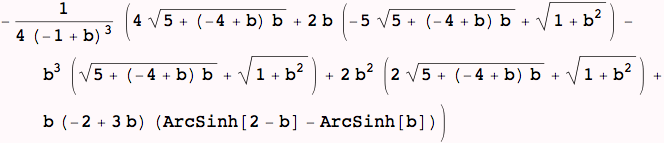
Visualizing the Approximation to the Brachiostone


As with the geodesic, illustrate the dependence of the approximating path for the brachistone and the total time.






The minimizer for b can be used to produce the quadratic approximation to the brachiostone and then plotted.


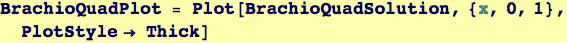

 = ∫
= ∫  dx
dx