"Textbook" Solutions to Second-Order Homogenous ODEs with Constant Coefficients

We write a general form for the left-hand-side of the homogeneous ODE with constant coefficients β and γ.

Guess a solution and substitute it into the left-hand side of the ODE:

This will be a solution when the resulting quadratic expression in λ is equal to 0:

Set the two solutions to λMinus and λPlus

The linear combination of the two solutiions is the general solution, here we set the two arbitrary constants.

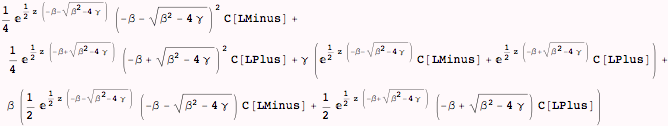
This will demonstate that our general solution is, in fact, a solution.

Created by Wolfram Mathematica 6.0  (16 November 2007)