Example of Transformation of Variables in Symbolic Differential Equations:The Bernoulli Equation

The Bernoulli equation is a first-order nonlinear ODE that has a form that can be reduced to a linear ODE as described in Kreyszig

The substitution y(x) = is made, resulting in a linear ODE that can be solved for u(x):

Here we define symbols that will be used in a subsequent rule-replacement method

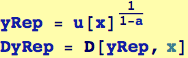
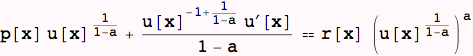
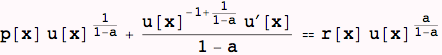
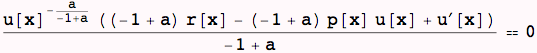
This is the form of the linear homogeneous first-order ODE for which we found the general solution above.

This last result is the first-order linear ODE that results from the Bernoulli equation. Its solution gives the function u(x) which can be converted back to y(x) with the relation y(x) = .

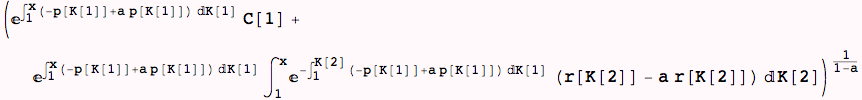
Created by Wolfram Mathematica 6.0  (13 November 2007)